Find the final velocity of the block

[MARK STRETERS]

Homework Statement

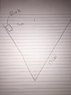
So here is the problem, There is a .03kg block that is in an inverted cone, the cone has a slant length of 15 cm and a radius of 4 cm, and the coefficient of friction is .35. The block rotates around the inside of the cone, seamlessly, until it hits the bottom of the cone. That is all we are given and we are supposed to find the final velocity of the block right before it hits the bottom of the cone. The picture attached is accurate except imagine that the cone is 3d and the block is moving in a circular motion around the edges of the cone. I have tried this numerous ways and each time I get an irrational answer.

Homework Equations

Ff= (mu)(mg)(costheta)
Vf^2= Vo^2 + 2a(X-Xo)
Vf= Vo +at

The Attempt at a Solution

I found the velocity of the block were it simply sliding down an inclined plane, pretty easy stuff, and I got 1.601 m/s for the final velocity. Its the centripetal/tangential acceleration that I'm having trouble with. What I did was I found what I think the tangential acceleration of the block using (mu)(Normal Force)/mass. If I did that correctly, I found the tangential acceleration to be .915 m/s^2. From there I used the kinematics equation vf= vo + at to find the final velocity. I found t from the equation t= √((2y)/a) using the height of the cone, .1446 cm, for y and .915 for a, and I found t to be .5621 seconds. So back to the kinematics equation vf= vo + at, I plugged in values and found vf= 0 + (.915)(.5621)= .514 m/s. So what I did from there was I plugged in the tangential final velocity and the final velocity of the block if it were down an inclined plane and plugged them into √((a)^2 + (b)^2)= √((1.601)^2 + (.514)^2) and got 1.68 m/s for the final velocity of the block, but I have no idea if that is correct. The picture below is accurate except imagine that the cone is 3d and the block is rotating around the inside of the cone.

 

[BvU]

Hi Mark,

What is theta ?
Do you realize that for an outsider this isn't decipherable ? You say "rotates" but rotation never reappears, yet "this is all we are given". There are no intial conditions either.

 

[MARK STRETERS]

Hi Mark,

What is theta ?
Do you realize that for an outsider this isn't decipherable ? You say "rotates" but rotation never reappears, yet "this is all we are given". There are no intial conditions either.

sorry, theta is 74.53 degrees. As for the whole rotates thing, this is as descriptive as our teacher was when giving us this problem. My problem statement isn't verbatim, but he never told us anything aside from what I have given. I am just as confused by this problem as you are.

 

[mfb]

How did you get the normal force?

I found the tangential acceleration to be .915 m/s^2

What did you assume for the direction of motion?

I found t from the equation t= √((2y)/a) using the height of the cone, .1446 cm, for y and .915 for a

How is the tangential acceleration related to time?

If you really have to consider a 3D motion in the cone, I would expect that both [the angle between "directly down" and the direction of motion of the object] and [the velocity] approach some constant that can be found. Brackets for clarity.

What are the initial conditions? If the block is not moving, there is no point in having the cone, it will just slide down an inclined slope.

 

[MARK STRETERS]

How did you get the normal force?
What did you assume for the direction of motion?
How is the tangential acceleration related to time?

If you really have to consider a 3D motion in the cone, I would expect that both [the angle between "directly down" and the direction of motion of the object] and [the velocity] approach some constant that can be found. Brackets for clarity.

What are the initial conditions? If the block is not moving, there is no point in having the cone, it will just slide down an inclined slope.

We weren't given any initial conditions other than that the block is set into motion around the cone. I was using an equation to find time so I could have all variables for the kinematic equation Vf=Vo + at

 

[mfb]

I was using an equation to find time so I could have all variables for the kinematic equation Vf=Vo + at

You cannot randomly use equations just because they have the right units.