Find the forces exerted by the floor and the wall at Q and R?

[devvaibhav]

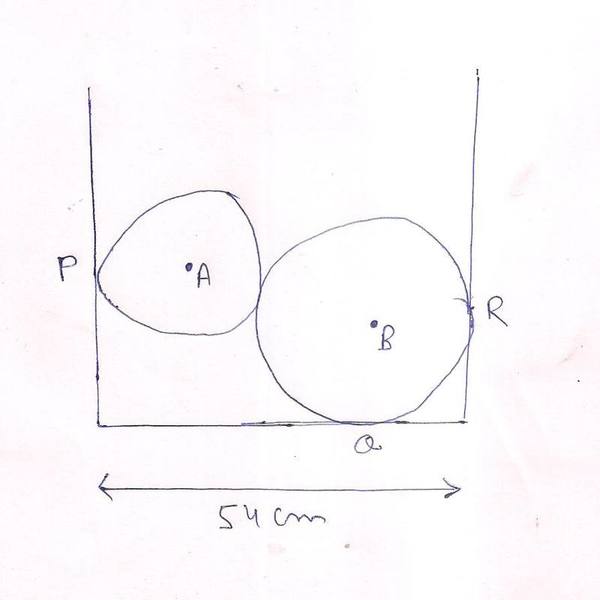
1. Two steel balls A and B are placed inside a right circular cylinder, of diameter 54 cm making contacts at points P, Q and R as shown in the figure. The radius r_A = 12 cm and r_B = 18 cm. The masses are m_A = 15 kg and m_B = 60 kg. The forces exerted by the floor at the point Q and the wall at R are ____ and ____(taking g = 10 m/s

Homework Equations

Sorry, it has no relevant equation. The concept is to draw free body diagrams and solve it..

The Attempt at a Solution

I have solved the force exerted by the floor at the point Q i.e. 750N. Please assist me with the second part.

Sorry for the disfigured circle...

 

[ehild]

Draw all forces. All are normal forces, normal to the walls or the ground, and those between the spheres are normal to the common tangent plane of the spheres and point toward the centres.

ehild

 

[devvaibhav]

@ehild sorry but i was unable to do it..please give some more explanation...

 

[phinds]

the statement "it has no relevant equation" is nonsensical. What would you solve if you had no equations to sovle? As ehid said, DRAW THE FORCES and then you'll have some equations.

Seems like the first part of the problem is to find out where P is and then where the spheres touch.

 

[ehild]

I drew a new figure. All forces (drawn by arrows) are either horizontal or vertical, except the force of interaction between the spheres. You need the angle of the yellow right triangle to find the horizontal and vertical components of this force. Try to do something.


ehild