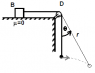
- #1
Vibhor
- 971
- 40
Homework Statement
Homework Equations
The Attempt at a Solution
The question says block B has negligible mass ,which means particle will be effectively in free fall i.e acceleration would be 'g' . But then it is given a horizontal velocity i.e it has centripetal acceleration ac about the pulley v2/r .
The forces acting on the particle are Mg and tension T .
So, Mg -T = M(√(g2+ac2))
I am really clueless with this problem .
Please help me .