Find the instant of the collision

[LCSphysicist]

Homework Statement

Two particles move about each other in circular orbits under the influence of gravitational forces, with a period τ. Their motion is suddenly stopped at a given instant of time, and they are then released and allowed to fall into each other. Prove that they collide after a time τ/4(2)^0.5

Relevant Equations

t = 2 pi a^1.5 * (m/k)^0.5
f = -Gmm/d^2

First of all, we can apply the third kepler of law, and call a by the major axis i.e, the distance between the particles.
Replacing μ = m1m2/(m1+m2)

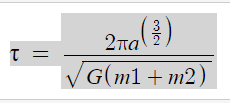
Now, the particle is distanced by a and is stopped, and, in a reference

r1 and r2 are the position of the particles, and r = r1-r2 their distance relative.

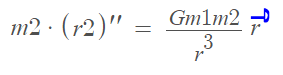
so

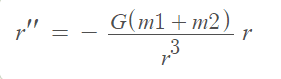
Period in this last equation and taking out the vectorial expression:

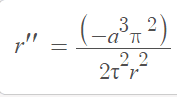
And, since r is relative distance, if i put r = 0, i would find the instant of the collision
BUT
I don't know how to deal with this strange differential equation x'' = C/x^2

 

[haruspex]

how to deal with this strange differential equation x'' = C/x^2

Can you think of something that you could multiply both sides by to make them both integrable?

 

[LCSphysicist]

Can you think of something that you could multiply both sides by to make them both integrable?

I thought of change of variables in the first term, we would have

dv dx = C/x²
dx dt

dv v = C/x²
dx

Solving>>

How to proceed?

I don't know if it can be done in elementary terms

 

[LCSphysicist]

I thought about attaching the problem by energy method, but since i am dealing with time, i choose approach by force.
Is my physics right until now? Maybe i forgot something

 

[haruspex]

I thought of change of variables in the first term, we would have

dv dx = C/x²
dx dt

dv v = C/x²
dx

Solving>>
View attachment 262862

How to proceed?

I don't know if it can be done in elementary terms

You can easily turn that into solving an integral, and don't forget C is negative, which is rather important.
For the integral, a change of variable can get the denominator into the form √(1-x²). This will give an affine numerator, but you can deal with the x and constant terms as separate integrals.

 

[ehild]

There is an easier approach using Kepler's third law.. Consider the situation as a single planet with reduced mass $\mu$ orbiting around the central mass m1+m2 along a circular orbit, with period T. If the planet losses speed, its orbit becomes elliptical with the central mass in the focus and the square of the time period changes as the cube of the semi-major axis. What is the orbit and its major axis if the planet moves along a straight line to the centre?

 

[LCSphysicist]

There is an easier approach using Kepler's third law.. Consider the situation as a single planet with reduced mass $\mu$ orbiting around the central mass m1+m2 along a circular orbit, with period T. If the planet losses speed, its orbit becomes elliptical with the central mass in the focus and the square of the time period changes as the cube of the semi-major axis. What is the orbit and its major axis if the planet moves along a straight line to the centre?

Oh well, now i see, it's a very physical approach, cool. thx

You can easily turn that into solving an integral, and don't forget C is negative, which is rather important.
For the integral, a change of variable can get the denominator into the form √(1-x²). This will give an affine numerator, but you can deal with the x and constant terms as separate integrals.

Thanks haruspex too by the help :)

 

[ehild]

I thought of change of variables in the first term, we would have

dv dx = C/x²
dx dt

dv v = C/x²
dx

Solving>>
View attachment 262862

How to proceed?

I don't know if it can be done in elementary terms

I think it is better to use positive constants and factor out all constants from the square root. Then you have $$\sqrt{\frac{r_0}{x}-1}$$ in the integral , which you can substitute by u.
Later, there can be an other, trigonometric substitution. But you can do it!

 

[LCSphysicist]

YEs, now i made by the way that i started. Actually i got to t = -τ/4(2)^0.5 maybe I've confused something, i will be looking.
Thank you all

 

[ehild]

YEs, now i made by the way that i started. Actually i got to t = -τ/4(2)^0.5 maybe I've confused something, i will be looking.
Thank you all

How did you do it? Show your work, please.

 

[LCSphysicist]

How did you so it? Show your work, please.

Here is my solution and me seeing this minus sign after all the work done.

 

[LCSphysicist]

How did you do it? Show your work, please.

Could you justify your solution? I see that i understand how to resolve by your [nice] method, but how justify these, like, why we can do it? It's a little intuitive to me think about the center of mass, but I can't prove it. Not in the case which the masses are comparable.

 

[PeroK]

Could you justify your solution? I see that i understand how to resolve by your [nice] method, but how justify these, like, why we can do it? It's a little intuitive to me think about the center of mass, but I can't prove it. Not in the case which the masses are comparable.

The idea is this. Consider the two body system with an initial separation of $r$. Consider a small angular momentum component, so that the masses do not collide, but follow a highly elliptical orbit. The initial separation $r$ becomes (approx) twice the semi-major axis of the ellipical orbit. And the time to collide becomes approximately half of the period of the highly ellipical orbit.

Then use Kepler's law to get the period of the highly elliptical orbit.

 

[ehild]

Could you justify your solution? I see that i understand how to resolve by your [nice] method, but how justify these, like, why we can do it? It's a little intuitive to me think about the center of mass, but I can't prove it. Not in the case which the masses are comparable.

The motion of two interacting bodies can be reduced to a single-body problem, of a body with the reduced mass orbiting around the central mass m1+m2, and this central mass is in rest in the centre-of mass system. The other things are Kepler's laws,and they can be also justified by solving Newton's equation .
Originally, the orbit is circular. If the planet losses speed at point P, the energy an angular momentum decreases. the blue orbit results. Finally, the planet losses all its speed and angular momentum. The orbit becomes the red one, a straight line segment. The focus is where the central mass is, it stays the same for all orbits.

The energy of the planet depends only on the major axis. If the planet loses energy, the length of the major axis diminishes. You can see all derivation concerning Planetary Motion in textbooks, or you can do it yourself.

 

[ehild]

View attachment 262938
Here is my solution and me seeing this minus sign after all the work done.

View attachment 262938
Here is my solution and me seeing this minus sign after all the work done.

Sorry, I cannot read and do not understand the integral of $$\frac{1}{\sqrt{\frac{r_0}{r}-1}}$$
By the way, your minus sign may come from the the first step when you find v(r) and take it positive, although it is negative with respect to vector r.

 

[haruspex]

View attachment 262938
Here is my solution and me seeing this minus sign after all the work done.

The integral $\int\frac{dr}{\sqrt{\frac{r_0}r-1}}$ is not $\sqrt{\frac{r_0}r-1}$.
I explained how to deal with it in post #5.

 

[LCSphysicist]

Actually i forgot to write the symbol of integral so became confused, and i lost the paper :| So, now i took the value in a calculator, what is the same that i find, except that i found.
:"-ro" and not "-*√ro√ro"

beingx = r,
k = ro