Find the missing force when the boy is pulled

[kuruman]

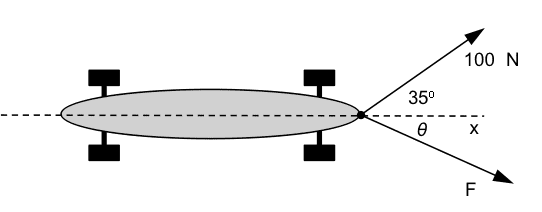
The skateboard as seen from above. It is rolling in the plane of the screen. The two forces are also in the plane of the screen and have no component perpendicular to the screen. The x-axis is horizontal. A picture is worth 2¹⁰ words.

On Edit: In part (b) we are told that they accelerate for 4 s. Starting from rest at an acceleration of 8.5 m/s², they would reach a speed of 34 m/s or 76 miles per hour! They must be using sports cars to pull the kid which constitutes reckless endangerment and child abuse. Don't ry this at home.

 

[issacnewton]

Ok, I think I did wrong calculation in post 28. We have $$F_2 \cos(35) + F_1\cos(\theta) = ma$$ and we also have $F_2\sin(35) = F_1\sin(\theta)$. This together leads to $$\tan(\theta) = \frac{F_2\sin(35)}{ma - F_2 \cos(35)} $$ Plugging $m = 17$ kg and $a= 8.5\; m/s^2$, we would get $\theta = 42.5$ degrees. And then $F_1 = F_2\sin(35)/\sin(\theta) = 84.9 N$. I hope this is correct.

 

[kuruman]

Your answer for part (a) agrees with mine.

 

[phinds]

But the problem is really confusing. It should explicitly tell the student what the question is talking about.

My view is that the problem is well formulated (it is a VERY common type of introductory mechanics problem) but you have given it a very weird and unexpected interpretation that is totally different than what just about everyone else would ever give it. When you have encountered a few more of these problems you'll see what I mean.

 

[kuruman]

My view is that the problem is well formulated (it is a VERY common type of introductory mechanics problem) but you have given it a very weird and unexpected interpretation that is totally different than what just about everyone else would ever give it. When you have encountered a few more of these problems you'll see what I mean.

My view differs somewhat from yours. I agree that, after seeing several of these problems, one acquires an intuitive understanding of how to interpret them. That's a sign that one has made the transition from novice to expert. However, I think that the formulator of a well crafted problem should look ahead for possible misunderstandings of the wording and include a figure if there is a possibility of misinterpretation by novices. I also think that the given acceleration is totally unrealistic and absurd. Numerical answers should provide an understanding and an estimating ability of the numbers associated with the quantities that are used. The formulator of this problem apparently did not pay attention to that aspect. For these reasons, I would say that this problem is so-so formulated.

 

[phinds]

For these reasons, I would say that this problem is so-so formulated.

Very reasonable. I didn't even look at the numbers but I have now and I agree w/ you.