- #1
issacnewton
- 1,000
- 29
Homework Statement
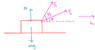
A 15.0 kg boy sits on a 2.00 kg stake board and is pulled forward by his parents. His mom pulls with a force of 100. N at an angle of 35 degrees and the boy and skate board accelerate along the x-axis at 8.50m/s2? a. What is the magnitude and direction of the father’s force if the boy and skate board move along the x axis? b. How far would they get if they started from rest and the parents pulled for 4.00s?
Homework Equations
Newton's law
The Attempt at a Solution
Let ##F_2 = 100 N## be the force exerted by the Mom and ##F_1## be the force exerted by the dad and let ##\theta## be the angle made by this with the horizontal. Let ##m## be the mass of the boy + stake board. The we have weight ##mg## and the normal reaction upward ##N## acting on boy+board system. We can set up the following equatons.
$$ F_1 \cos(\theta) + F_2 \cos(35) = ma$$
$$ 0 = N + F_2 \sin(35) + F_1 \sin(\theta) - mg$$
Now ##a## is also given, so we have 2 equations and three unknowns, ##F_1##, ##\theta##, and ##N##. So how would we solve this ?