jweica
- 5
- 1
New user has been reminded to use the Homework Help Template when starting schoolwork threads at the PF
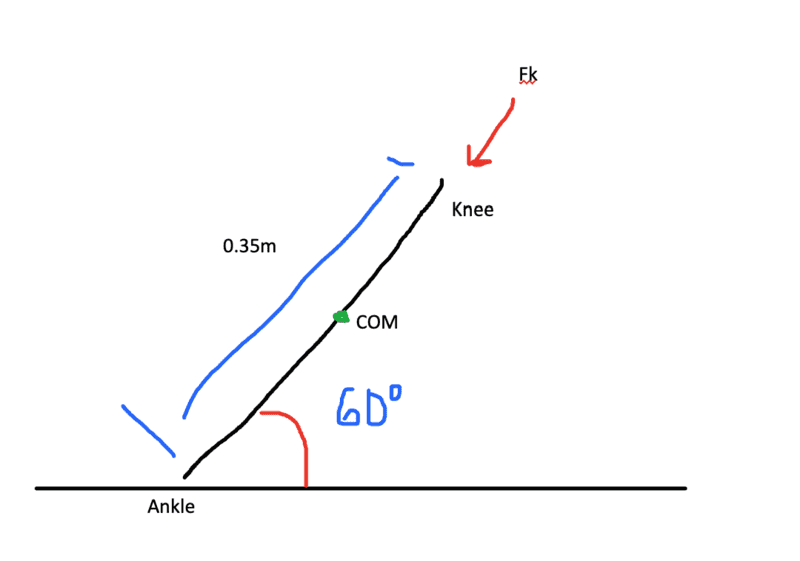
Given that the tibia is 0.6kg and is 35 cm long. The force at the knee (Fk) is: (-200i + 346.41j)N
Find the moment about the ankle due to Fk
I found that: r: rx = (0.35cos60) and ry = (0.35sin60)
Using the sum of moments where: rxFy - ryFx = 0
[(0.35cos60)(346.41)] - [(0.35sin60)(-200)] = 0 k Nm
But I am wondering since the tibia weighs 0.6kg, wouldn't that be included in the question as a Fy component [(0.6)(9.81) = -5.886]?
Do I neglect the weight and only use the Fk?
((I attached a poorly drawn free body diagram))
Find the moment about the ankle due to Fk
I found that: r: rx = (0.35cos60) and ry = (0.35sin60)
Using the sum of moments where: rxFy - ryFx = 0
[(0.35cos60)(346.41)] - [(0.35sin60)(-200)] = 0 k Nm
But I am wondering since the tibia weighs 0.6kg, wouldn't that be included in the question as a Fy component [(0.6)(9.81) = -5.886]?
Do I neglect the weight and only use the Fk?
((I attached a poorly drawn free body diagram))
