Find the Riemannian curvature tensor component

[Tom Weaver]

Given the metric of the gravitational field of a central gravitational body:

ds² = -e^v(r)dt² + e^μ(r)dr² + r² (dθ² + sin²θdΦ²)

And the Chritofell connection components:

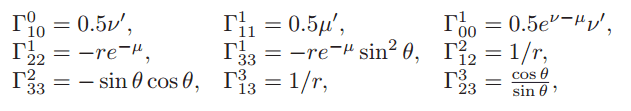
Find the Riemannian curvature tensor component R⁰₁₁₀ (which is non-zero).

I believe the answer uses the Ricci tensor:

R_μv = R^λ_μvλ = Γ^λ_μλ,v - Γ^λ_μv,λ + Γ^ρ_μλΓ^λ_vρ - Γ^λ_μvΓ^ρ_λρ

This is far as I've got:

R⁰₁₁₀ = Γ⁰_10,1 - Γ⁰_11,0 + Γ^ρ₁₀Γ⁰_1ρ - Γ⁰₁₁Γ^ρ_0ρ

R⁰₁₁₀ = 0.5v'' + Γ^ρ₁₀Γ⁰_1ρ - Γ⁰₁₁Γ^ρ_0ρ

I'm not entirely sure on the meaning of ρ, at first I thought it would cycle through 0, 1, 2 and 3 to represent the 4 dimensions but after working that through I found it didn't work. Any help is much appreciated!

 

[TSny]

I believe the answer uses the Ricci tensor:

R_μv = R^λ_μvλ

Hello.

The summation convention implies that the right-hand side is summed over $\lambda = 0, 1, 2, 3$. You cannot just set $\lambda = 0$ on the right-hand side (and $\mu = 1$, $\nu = 1$) in order to claim that $R_{11} = R^0_{\; 110}$.

 

[Tom Weaver]

Hello.

The summation convention implies that the right-hand side is summed over $\lambda = 0, 1, 2, 3$. You cannot just set $\lambda = 0$ on the right-hand side (and $\mu = 1$, $\nu = 1$) in order to claim that $R_{11} = R^0_{\; 110}$.

Brilliant thank you! Am I right at least in using the Ricci tensor? If so, what's the significance of ρ?

 

[TSny]

In the Ricci tensor, $\rho$ is a repeated index. So it plays the role of a summation index.

I don't see how the Ricci tensor is going to be helpful for this problem. Instead, use the fundamental expression for $R^\mu_{\; \nu \alpha \beta}$ in terms of the Christoffel symbols.

 

[Tom Weaver]

R^ρ_λμν = - Γ^ρ_λμ,ν + Γ^ρ_λν,μ - Γ^σ_λμΓ^ρ_σν + Γ^ρ_λνΓ^ρ_σμ

R⁰₁₁₀ = - Γ⁰_11,0 + Γ⁰_10,μ1 - Γ^σ₁₁Γ⁰_σ0 + Γ^σ₁₀Γ⁰_σ1

R⁰₁₁₀ = - (Γ⁰₁₁Γ⁰₀₀ + Γ¹₁₁Γ⁰₁₀ + Γ²₁₁Γ⁰₂₀ + Γ³₁₁Γ⁰₃₀) + (Γ⁰₁₀Γ⁰₀₁ +Γ¹₁₀Γ⁰₁₁ + Γ²₁₀Γ⁰₂₁ + Γ³₁₀Γ⁰₃₁)

R⁰₁₁₀ = - (0 + 0.5v'*0.5μ' + 0 + 0) + ((0.5v')² + 0 + 0 + 0)

R⁰₁₁₀ = (0.5v')² - 0.25 ν' μ'

I'm still unsure of what σ is, again, thank you for your help.

 

[TSny]

R^ρ_λμν = - Γ^ρ_λμ,ν + Γ^ρ_λν,μ - Γ^σ_λμΓ^ρ_σν + Γ^ρ_λνΓ^ρ_σμ

You have a typographical error in the last term. Can you spot it?

R⁰₁₁₀ = - Γ⁰_11,0 + Γ⁰_10,μ1 - Γ^σ₁₁Γ⁰_σ0 + Γ^σ₁₀Γ⁰_σ1

OK, except for the $\mu$ subscript in the second term on the right. Did you mean for that to be there? When going to the next line (3rd line in your post), you have dropped the first two terms of the second line. Although one of these terms is zero, the other one is not zero. Every thing else looks OK to me. So, I think your final result is correct except for the term that you dropped that is not zero.

I'm still unsure of what σ is, again, thank you for your help.

$\sigma$ is a summation index because is appears twice in a term; once as a superscript and once as a subscript. It looks to me that you handled $\sigma$ correctly.

 

[Tom Weaver]

Great thank you! Your help is greatly appreciated!