Find the upward acceleration of the man

[avistein]

Homework Statement

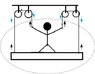
A man of mass m stands on a platform of equal mass m and pulls himself by two ropes passing over pulleys.If he pulls each rope with a force to half its weight,his upward acceleration would be

a)g/2
b)g/4
c)g
d)0

The Attempt at a Solution

force exerted by man=1/2mg*2=mg
total force exerted downwards=mg+mg=2mg(weight of man and platform)
then 2mg-mg=2ma=>a=g/2
But answer given is 0.How?

 

[Doc Al]

Consider the man + platform as a single system. How many upward forces act on that system?

 

[avistein]

Cant find it .please help.

 

[avistein]

Ok.downward force is mg+mg=2mg

 

[avistein]

2 upward force act.

 

[Doc Al]

2 upward force act.

No. Draw an imaginary box around the 'man + platform'. How many rope segments attach to (and thus pull up on) that system?

 

[BvU]

Let me also ask a "helping" question: Consider the man by himself. He is pulling straight down on two ropes, each with a force equal to half his weight X g. How much force does he exercise on the platform in a static situation ?

 

[avistein]

2 rope segments.

 

[BvU]

Ah, posts cross. You want me to pick up on doc's line of approach?

 

[avistein]

both your and doc's.

 

[BvU]

2 rope segments.

I would say four. A segment would be something that exercises a force. A piece of rope slung around a pulley attached to a ceiling can exercise two upward forces, so it's convenient to speak of two segments.

 

[avistein]

@Bvu,he exercise mg force.

 

[avistein]

@Bvu,then each rope has two segments,right?

 

[BvU]

Now the fun thing about a segment of rope in physics is that a) it's weightless ;-) and b) tension forces at each end are equal. That way a piece of rope can be treated as one, but I just talked myself into looking at them as two segments. Doc will decide what's wisdom here. We don't let this hold us back.

So we have four segments pulling up, each with mg/2 (m = man's mass). Right ?

 

[BvU]

Now we have to complete the man+platform picture. What other forces play a role ?

Spoiler

(rhetorical, you already answered) mg down for the man, mg down for the platform (m=mass platform=mass man)

 

[avistein]

@Bvu,if there are two pulleys then will the segments be 2?

 

[avistein]

@Bvu,I do not understand that why do we need to consider the mg/2 two times in a single rope?

 

[BvU]

@Bvu,if there are two pulleys then will the segments be 2?

My reasoning would be 4. So yes, here you could claim that there are 8 segments and we only see 6 chunks of rope. Talked myself in a corner there...

In the picture the two pulleys on the left do exactly the same as one pulley would do. Same for the two on the right. Drawing two each is somewhat sadistic on the part of the composer of the exercise.

My argument for the sections is that a section can exercise a force in a direction. Two sections of a chunk of rope slung around a pulley exercise two forces of equal magnitude but different directions. (Viz. the pulley at the top of the 30 degree ramp earlier).

Here e.g. the leftmost pulley pulls up on the platform and pulls to the left on the second pulley.
The second pulley pulls to the right on the first and pulls up on the man.

This way I bluf my way into considering the piece of rope between the two pulleys as two sections. Others might beg to disagree.

 

[BvU]

@Bvu,I do not understand that why do we need to consider the mg/2 two times in a single rope?

This is starting to look like a typing contest... I'm old and I'm slow typing with only two fingers...

The idea is already in my preceding post: it can exercise two forces, one at each end. Because of pulleys the directions can be equal or different.

 

[BvU]

@Bvu,he exercise mg force.

Ah, you fell for the trick question. Half his weight on each of the ropes leaves nothing for the platform !

 

[BvU]

So here's the drawing doc hoped you would make. The imaginary box is the dotted ellipse ;-).
And you see straight away why I adopted that working definition of a segment. I start liking it more and more!

Now back to business and an answer to the question you deftly circumnavigated: what other forces play a role on the system in the dotted ellipse ?

 

[avistein]

and why tension will be equal to mg/2?

 

[BvU]

and why tension will be equal to mg/2?

That's what it said in the original problem, right ?

I see, it said half its weight, which is half the weight of the platform which is half the weight of the man.

edited:
[strike]Your part of the world may be handicapped by thinking weight and force have the same dimension. They do not.Weight = mass,[/strike]

On second thought -- or rather after thinking -- a bigger part of the world is handicapped by this weight/mass difference that daily language use ignores. Let me speak for myself only in the future!​

Force = mass X acceleration.

In decent units: My [strike]weight[/strike] mass is 100 kg, sadly. If I hang from a rope attached to a firm branch, the tension in the rope is 100 kg * 9.81 m/s². At my position (either hands or feet, rather not: neck) that force is pulling up, at the branch it is pulling down.

 

[Doc Al]

and why tension will be equal to mg/2?

Because you are told that the man pulls each rope with a force of mg/2. That means the rope must be pulling back on him with an equal force (Newton's 3rd law) and thus that the tension in the rope must equal mg/2.

 

[BvU]

Hi doc. You take over, please.

 

[avistein]

suppose there is a pulley with one end hangs a mass m1 and other end hangs a mass m2(m2>m1).then why do we write m2g-T=m2a and T-m1g=m1a? In this case also T should be same as the force pulling the string? that is T=m2g?? then why not?

 

[Doc Al]

suppose there is a pulley with one end hangs a mass m1 and other end hangs a mass m2(m2>m1).then why do we write m2g-T=m2a and T-m1g=m1a? In this case also T should be same as the force pulling the string? that is T=m2g?? then why not?

Yes, T is the same as the force pulling on the string at each end. But that force doesn't equal m2g. (Or m1g. Don't forget that the other end of the string has a mass m1 hanging from it.)

Just because a mass m2 hangs from a string does not mean that the mass exerts a force equal to its weight on the string. Realize that the mass is accelerating. That's why we need to apply Newton's 2nd law and solve for the tension and the acceleration.

In this problem (the one you started this thread about) you are told the tension that the ropes must exert.

 

[avistein]

Yes, T is the same as the force pulling on the string at each end. But that force doesn't equal m2g. (Or m1g. Don't forget that the other end of the string has a mass m1 hanging from it.)

Just because a mass m2 hangs from a string does not mean that the mass exerts a force equal to its weight on the string. Realize that the mass is accelerating. That's why we need to apply Newton's 2nd law and solve for the tension and the acceleration.

In this problem (the one you started this thread about) you are told the tension that the ropes must exert.

But here also the other end has some mass(mass of man+platform).And why in this case we are considering that the system is at rest?

 

[avistein]

We can consider the force exerted by the man is same as the weight hanging from one end.right?

 

[Doc Al]

But here also the other end has some mass(mass of man+platform).

So? Each end of the rope attaches to the 'man + platform'. Since 4 ends exert their tension on the system, the total upward force is 4 x mg/2 = 2mg.

And why in this case we are considering that the system is at rest?

The system is not necessarily at rest. By applying Newton's 2nd law, you can calculate that the acceleration is zero.

 

[Doc Al]

We can consider the force exerted by the man is same as the weight hanging from one end.right?

I don't know what you mean.

Here we are told how hard he pulls. So the tension is given.

In the case of a hanging mass, you are not told the tension you have to figure it out.

 

[BvU]

We can consider the force exerted by the man is same as the weight hanging from one end.right?

If I try to be a good listener (something like a lawyer trying to clear you), I could say: somewhat, given the very unfortunate wording of the original problem:

If he pulls each rope with a force to half its weight

[strike]That can not be in the law book of physics, because the dimensions are different. You may want to check on that wording. I already sneered at that in post #23. Doc backs me up. But for now I take your word that that is how it was mischievously (actually: wrongly) formulated. But[/strike] it means m/2 times g and that way we have a force [strike]again.[/strike]

And your the "weight hanging from one end" would then mean: the tension force at the lower end of e.g. the rightmost rope. Also a force. "Weight hanging from one end" [strike]times g[/strike] is only almost right. The m/2 times g trick doesn't work here, because we have not yet established that there is no acceleration ! the factor 2 can be admitted because of the symmetry. But the factor g has to be (g - a).

Do you think you now have enough to rephrase in a way that Doc doesn't have a chance to claim he doesn't know what you mean ? Your idea is right (I think), but the formulation leads to an answer like his (for your own good!).

 

[Doc Al]

That can not be in the law book of physics, because the dimensions are different. You may want to check on that wording.

I suspect it's a typo.
It should read:

If he pulls each rope with a force to half [STRIKE]its[/STRIKE] his weight

 

[BvU]

I stand corrected. So often seen weight expressed in kg that it deformed me. And then sneering at lb and lbf speaking nations. I should be ashamed and I am !

Feels great, though, because --being quite asine-- I won't make that mistake any more...

Also a bit obnoxious: his weight happens to be its weight (the platforms weight). Mightily confusing for our avi.

 

[avistein]

If he pulls each rope with a force to half its weight

It's a typo.It should be "half his weight".

But here in the man+platform problem,how can we consider that the force applied by the man has no acceleration? then only we can write T-mg/2=0=>T=mg/2

Suppose a pulley is there and one end has a mass and the other end has a force exerted by the man.Then here also will the tension equal to the force applied ? Then why not the tension=force when the force is replaced by a mass?

 

[avistein]

because we have not yet established that there is no acceleration

But here in the man+platform problem,how can we consider that the force applied by the man has no acceleration? then only we can write T-mg/2=0=>T=mg/2

 

[Doc Al]

But here in the man+platform problem,how can we consider that the force applied by the man has no acceleration? then only we can write T-mg/2=0=>T=mg/2

You do not assume no acceleration. You apply Newton's 2nd law and deduce it. (Here you are told that T = mg/2.)

 

[BvU]

Ah, now we are back to the original exercise somewhat. The idea is that you draw all the forces, including the gravitational forces (ahem, the weights). With the pulleys transferring the man's pulling force to the tensions in the ropes to the platform, you then have all that is needed to establish the acceleration of the platform. And then you will find ...

So: back to business and an answer to the question: what other forces play a role on the system in the dotted ellipse ? (post #21)

 

[BvU]

But here in the man+platform problem,how can we consider that the force applied by the man has no acceleration? then only we can write T-mg/2=0=>T=mg/2

Could it be that there is something in the concept of a tight rope -- with or without a pulley -- that hasn't completely settled in your mind? Just a hunch on my part, and believe me: it is so common and so basic that it is very, very often overseen.

So pardon me if I repeat the obvious (it will be of use many more times in PF, anyway):

In statics and in dynamics a tight, massless rope

• transfers force from one end to the other end.
  
  you pull the rope, the rope pulls whatever is attached at the other end​
• the forces on each end are equal and opposite
  
  Like action = - reaction at a distance
  the magnitudes of the forces must be exactly equal
  otherwise the rope itself would accelerate (with "infinite" acceleration, according to ΔF = ma)​
• the forces are aligned with the rope
  otherwise the rope would move sideways
  

  (Try it: push sideways against a dangling rope!)​

  If the rope is slung over a pulley, this is still true for all sections of the rope
  (a section is a straight piece of rope with a distinct direction
  -- it can be considered as a separate rope attached to something else
  -- the something else can also be a section of rope)
  ​

(open for clarifications, error correction, further questions)