- #1
jaychay
- 58
- 0
Can you please help me ?
I have tried to do it but I end up getting the wrong answer.
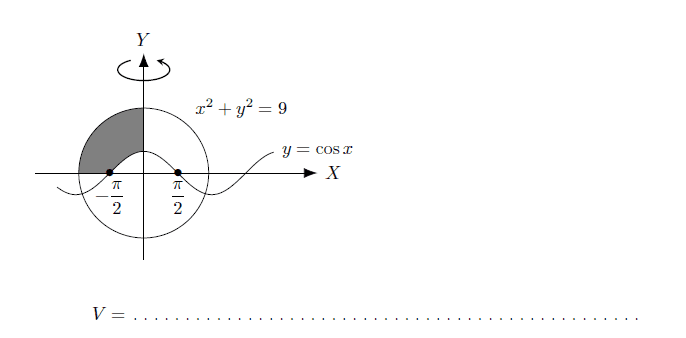
I have tried to do it but I end up getting the wrong answer.