SUMMARY
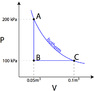
The discussion focuses on calculating the work done on a monoatomic gas using a P-V diagram. Key equations include the internal energy change formula, $$\Delta U = \frac{3}{2}nR(T_2 - T_1)$$, and the work done, $$W = P\Delta V$$. Participants clarify that the total work done in a cycle is represented by the area under the curve, specifically for the BC leg, which is calculated as a trapezoid. The correct values for pressure and volume at points A, B, and C are critical for accurate calculations.
PREREQUISITES
- Understanding of the ideal gas law and its applications.
- Familiarity with thermodynamic concepts, particularly internal energy and work.
- Knowledge of calculus, specifically integration techniques for area under curves.
- Ability to interpret P-V diagrams and calculate areas geometrically.
NEXT STEPS
- Study the derivation and application of the ideal gas law in thermodynamic processes.
- Learn how to calculate work done in thermodynamic cycles using integration.
- Explore the relationship between internal energy, heat, and work in thermodynamics.
- Investigate the properties of monoatomic gases and their behavior under various conditions.
USEFUL FOR
Students and professionals in physics, particularly those focusing on thermodynamics, engineers working with gas systems, and anyone involved in energy calculations in mechanical systems.