Femme_physics
Gold Member
- 2,548
- 1
Homework Statement
Find the coordinates of point A and B
The function is
f(x) = x2 -6x +a
(where "a" is a parameter)
The equation tangent line to the function at point A is
y = -2x +1
The equation tangent line to the function at point B
y = 2x -11
http://img864.imageshack.us/i/calc01.jpg/
The Attempt at a Solution
In order to find A I just need to set the function equal to the line equation at A, since this is the point where they meet. The problem is that "a" is a parameter. Until I know a I can't solve this equation. I can see "a" as an unknown, but then I got 1 equation and 2 unknowns.
I'm rather confused as to how to find this point without "a" being defined to me.
Any help?
Last edited by a moderator:

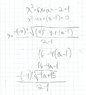


 )
)
