Finding a vector; need work checked

[Whitishcube]

Homework Statement

Find a vector of length 7 in the direction opposite to (-3,4)^T

Homework Equations

The Attempt at a Solution

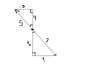
So i start off by drawing the vector (-3,4)^T (the T power meaning transposed), and then drawing a vector in the opposite direction of length 7. The first vector has a length of 5. My method involved separating each vector into its components and making two triangles out of them, and then using ratios involving the two known components of the first vector (-3 and 4), the components of the second vector (dubbed v_1 and v_2), and the lengths of each vector (5 and 7). The answer I got was v_1 = (-21/5) and v_2=(28/5).

I have included a picture in the attatchment. Thank you.

 

[rock.freak667]

You complicated this problem by over thinking.

if -a is opposite in direction to a, then what vector is opposite to -3i+4j ?

Then consider that any vector in this same direction will be a scalar multiple of this vector, you want its magnitude to be 7.

 

[Whitishcube]

I see what you mean haha. I'm new to the thinking in linear algebra. I got 21/5i and -28/5j for the vector. Is that correct?

 

[Mark44]

It's easy enough to check. Your vector should have a length of 7, and should be a multiple of <3, -4>.

 

[Whitishcube]

Yup. Checks out. Thanks!