Finding $\angle MBC$ in Triangle $ABC$ with Proof

[anemone]

Given a triangle $ABC$ such that $\angle BAC=103^{\circ}$ and $\angle ABC=51^{\circ}$. Let $M$ be a point inside triangle $ABC$ such that $\angle MAC=30^{\circ}$, $\angle MCA=13^{\circ}$.

Find $\angle MBC$ with proof.

 

[Albert1]

Given a triangle $ABC$ such that $\angle BAC=103^{\circ}$ and $\angle ABC=51^{\circ}$. Let $M$ be a point inside triangle $ABC$ such that $\angle MAC=30^{\circ}$, $\angle MCA=13^{\circ}$.

Find $\angle MBC$ with proof.

my solution:

Spoiler

View attachment 1817
from the sketch it is easy to prove that $\angle MBC=17^o=y=\dfrac {\angle ABC}{3}$

 

[mente oscura]

my solution:

Spoiler

View attachment 1817
from the sketch it is easy to prove that $\angle MBC=17^o=y=\dfrac {\angle ABC}{3}$

Hello.

Could you show it?.

I have managed to find out, only:

Spoiler

\overline{OC}=, angle bisector of \angle ACB

certain angles: 13, 26, 30, 34, 43, 51, 56, 60, 64, 73, 77, 103, 116, 129.

Regards.

Edit: I'm sorry. I had not seen, before, that it was already drawing.

 

[Opalg]

[sp]

my solution:

View attachment 1817
from the sketch it is easy to prove that $\angle MBC=17^o=y=\dfrac {\angle ABC}{3}$

In case there are other people like me who took a while to follow Albert's clever proof, here is how it works. You are given the angles of triangle ABC: $103^\circ$ at A, $51^\circ$ at B and therefore $26^\circ$ at C. You are also given the angles of triangle AMC: $30^\circ$ at A, $13^\circ$ at C and therefore $137^\circ$ at M. Since 13 is half of 26 it follows that MC bisects the angle at C. So if we drop perpendiculars E, F from M to AC and BC, the right-angled triangles MEC, MFC will be congruent, with angle $77^\circ$ at M. Now draw the circle centred at M touching AC, BC at E and F, and let BG be the other tangent to the circle from B. Then the right-angled triangles BFM, BGM are congruent. At this stage we know the angles $60^\circ$, $77^\circ$, $77^\circ$ at M. So the remaining angle AMF is $146^\circ$ and this is bisected by BM. Therefore the angle BMF is $73^\circ$; and its complement, the angle MBC, is $17^\circ.$[/sp]

 

[johng1]

Opalg, maybe you can enlighten me about Albert's proof. I fail to see why G, the intersection of AM with the circle, must be a tangent point from B. I had played with the problem before looking at the solution and came up with the following:

View attachment 1821
So an indirect proof follows by showing the given construction must be the triangles as given in the problem. I think this is right.

 

[Opalg]

Opalg, maybe you can enlighten me about Albert's proof. I fail to see why G, the intersection of AM with the circle, must be a tangent point from B...

That is a very good point, which I had completely overlooked. The only way round it that I can see is to do essentially as you suggest. Namely, suppose that the tangent at G meets the line BC at some point B', and then show that B'=B.

 

[Albert1]

MG is a radius , so $\angle BGM=90^o$

MG is a tangent line of circle M

here point M is the incenter of triangle BHC

 

[Opalg]

MG is a radius , so $\angle BGM=90^o$

MG is a tangent line of circle M

here point M is the incenter of triangle BHC

That implies that you are defining G as the point where the tangent from B meets the circle. In that case, you need to explain why G lies on the line AM.

 

[Albert1]

$\angle FBG=\dfrac{77+77+60-146}{2}=34^o$

$\therefore \angle GBA=17^o$

and $\angle AGB=180-73-17=90^o$

 

[Opalg]

$\angle FBG=\dfrac{77+77+60-146}{2}=34^o$

$\therefore \angle GBA=17^o$

and $\angle AGB=180-73-17=90^o$

Yes, that seems to work. You are saying that the angles BAG and BAM are both $73^\circ$. So G (defined as the point where the tangent from B meets the circle) lies on the line AM.

I think this discussion shows that these "proofs by picture" are inadequate on their own. Unless they are accompanied by a careful explanation of how each constructed point is defined, together with the order in which deductions are made, the structure of the proof is almost impenetrable.

 

[johng1]

Albert, Opalg, someone please help. I still don't get it. In Albert's expression for angle BFG, the 77+77+60 is the angle AME, but from where comes 146?? Is he saying triangle AMB is isosceles?

The following sketch shows G' as the second tangency point from B and G the intersection of AM with the circle. I still fail to see why G = G'. (Of course the drawing is not accurate; the actual problem has G = G'.)

View attachment 1826

 

[Albert1]

146=360-77-77-60

 

[mente oscura]

146=360-77-77-60

Yes, but the problem is that prove that it are those angles and not others

 

[anemone]

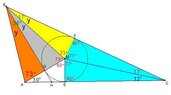
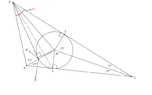
First off, my first thank goes to Albert, for you provided a proof with diagram in this challenge problem. But, like others, I have a really hard time to digest your proof and I must look at the follow-up post by Opalg to fully decipher the reasoning behind your proof. Still, I am struggling to see why there must be true that the line $BGH$ is a tangent to the circle at the point $G$. I am sorry...

I want to also thank to Opalg, for your willingness to answer to johng's posts, because I always think it's the OP's responsibility to answer to anyone who has found the proof confounding...

My solution:

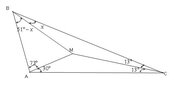
View attachment 1834
Ceva's theorem tells us the product of the ratios of the pairs of segments formed on each side of the triangle by the intersection point is equal to 1.

Hence we have

$\dfrac{\sin 13^{\circ}}{\sin 13^{\circ}} \cdot \dfrac{\sin 73^{\circ}}{\sin 30^{\circ}} \cdot \dfrac{\sin x}{\sin (51^{\circ}-x)}=1$

$\sin 73^{\circ}\cdot \sin x=\sin 30^{\circ} \cdot \sin (51^{\circ}-x)$

$\sin 73^{\circ}\cdot \sin x=\sin 30^{\circ} \cdot (\sin 51^{\circ} \cos x-\cos 51^{\circ} \sin x)$

$\sin x(\sin 73^{\circ}+\sin 30^{\circ}\cos 51^{\circ})=\sin 30^{\circ} \sin 51^{\circ} \cos x $

$\begin{align*}\tan x&=\dfrac{\sin 30^{\circ} \sin 51^{\circ}}{\sin 73^{\circ}+\sin 30^{\circ}\cos 51^{\circ}}\\&=\dfrac{\dfrac{1}{2} \sin 51^{\circ}}{\sin 73^{\circ}+\dfrac{1}{2}\cos 51^{\circ}}\\&=\dfrac{\sin 51^{\circ}}{2\sin 73^{\circ}+\cos 51^{\circ}}\\&=\dfrac{\sin 3(17)^{\circ}}{2\sin (90-17)^{\circ}+\cos 3(17)^{\circ}}\\&=\dfrac{\sin 17^{\circ}(3-4\sin^2 17^{\circ})}{2\cos 17^{\circ}+\cos 17^{\circ}(4\cos^2 17^{\circ}-3)}\\&=\dfrac{\sin 17^{\circ}(3-4\sin^2 17^{\circ})}{\cos 17^{\circ}(2+4\cos^2 17^{\circ}-3)}\\&=\dfrac{\sin 17^{\circ}(3-4\sin^2 17^{\circ})}{\cos 17^{\circ}(4(1-\sin^2 17^{\circ})-1)}\\&=\tan 17^{\circ}\end{align*}$

$\therefore x=17^{\circ}$

 

[Opalg]

Albert, Opalg, someone please help. I still don't get it. In Albert's expression for angle BFG, the 77+77+60 is the angle AME, but from where comes 146?? Is he saying triangle AMB is isosceles?

The following sketch shows G' as the second tangency point from B and G the intersection of AM with the circle. I still fail to see why G = G'. (Of course the drawing is not accurate; the actual problem has G = G'.)

View attachment 1826

Yes, you are right again, and this time I don't see any way to fix it. The distorted diagram showing G and G' as distinct points highlights the difficulty in Albert's argument. Fortunately, anemone has now given us a watertight proof using Ceva's theorem.

 

[Albert1]

View attachment 1837

hope this time you can understand it

 

[anemone]

View attachment 1837

hope this time you can understand it

Ah, I applaud your constant effort to try to show us the reasoning behind your work...but Albert, I only managed to follow up to where you mentioned why $G$ is the midpoint of $AM$, and I don't see how that would imply the two lines $BG$ and $AM$ are perpendicular to one another.

Also, if I could decipher that, what follows immediately is that the two triangles $BGA$ and $BGM$ are congruent triangles and hence $\angle ABM=180^{\circ}-2(73^{\circ})=34^{\circ}$ and that gives $\angle MBC=51^{\circ}-34^{\circ}=17^{\circ}$.

 

[Albert1]

Ah, I applaud your constant effort to try to show us the reasoning behind your work...but Albert, I only managed to follow up to where you mentioned why $G$ is the midpoint of $AM$, and I don't see how that would imply the two lines $BG$ and $AM$ are perpendicular to one another.

Also, if I could decipher that, what follows immediately is that the two triangles $BGA$ and $BGM$ are congruent triangles and hence $\angle ABM=180^{\circ}-2(73^{\circ})=34^{\circ}$ and that gives $\angle MBC=51^{\circ}-34^{\circ}=17^{\circ}$.

please see post #9

 

[anemone]

Using your diagram and if it were up to me, I would continue, after I realized $G$ is the midpoint of $AM$, by using the trigonometric approach! Please pardon me because to prove something using only geometrical approach is my downfall.

My solution to determine the $\angle BGA=90^{\circ}$ would be as follow:

Since $AG=GM=r$, therefore we have $AM=2r$. If we consider the triangle $AMC$, using the Sine Rule we get $\dfrac{AC}{\sin (60+77)^{\circ}}=\dfrac{AM}{\sin 13^{\circ}}$, or, $AC=\dfrac{2r\sin 137^{\circ}}{\sin 13^{\circ}}$.

Again, by applying Sine Rule to the triangle $ABC$ gives

$\dfrac{AB}{\sin 16^{\circ}}=\dfrac{AC}{\sin 51^{\circ}}$, or, $AB=\dfrac{2r\sin 137^{\circ}\sin 26^{\circ}}{\sin 13^{\circ}\sin 51^{\circ}}$.

Next, we need to find the length of $BG$ and this could be done by applying Cosine Rule to the triangle $BAG$:

$BG^2=AG^2+AB^2-2(AG)(AB)\cos 73^{\circ}$

$\therefore BG=3.27085r$

Last, we could find the value for $\angle BGA$ by using the Sine Rule again:

$\dfrac{AB}{\sin \angle BGA}=\dfrac{BG}{\sin 73^{\circ}}$

This shows that $\angle BGA$ is indeed, $90^{\circ}$!(Tmi)(Sun)

 

[Opalg]

please see post #9

Post #9 states that $\angle FBG=\dfrac{77+77+60-146}{2}$. I believe that is the step that several of us find incomprehensible. Could you explain it please?

 

[Albert1]

Post #9 states that $\angle FBG=\dfrac{77+77+60-146}{2}$. I believe that is the step that several of us find incomprehensible. Could you explain it please?

View attachment 1839

 

[johng1]

I promise this is my last post to this thread. It is basically my post 5, but I am now happy with the proof. (Of course the figure as drawn is inaccurate.)

View attachment 1840