SUMMARY
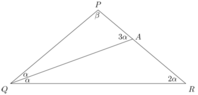
The problem involves finding angle P in isosceles triangle PQR, where PQ equals PR. The angle bisector at Q intersects PR at A, and the relationship QR = QA + PA is established. By applying the sine rule, it is determined that angle α equals π/9, leading to angle β being 5π/9 or 100 degrees. The solution is confirmed through trigonometric identities and the addition formula.
PREREQUISITES
- Understanding of isosceles triangles and their properties
- Knowledge of the sine rule in triangle geometry
- Familiarity with angle bisectors and their implications
- Proficiency in trigonometric identities and formulas
NEXT STEPS
- Study the sine rule in-depth, particularly in non-right triangles
- Explore properties of isosceles triangles and angle bisectors
- Learn about trigonometric identities and their applications in geometry
- Investigate the addition formulas for sine and cosine functions
USEFUL FOR
Mathematicians, geometry enthusiasts, and students studying trigonometry and triangle properties will benefit from this discussion.