Finding Current in a Parallel RLC Circuit

[Drakkith]

Homework Statement

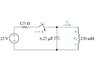
Find i_o for t≥0.
Express your answer in terms of t, where t is in milliseconds.

There is no energy stored in the circuit in (Figure 1) when the switch is closed at t = 0.

Homework Equations

$x(t)=x_f+[B_1cos(ω_dt)+B_2sin(ω_dt)]e^{-αt}$

The Attempt at a Solution

Let $i_R$ be the current through the resistor, $i_c$ be the current through the capacitor, and $V_c$ be the voltage across the capacitor.
At $t=0$:
No energy is stored in the circuit, so $V_c(t<0)=0$, $i_o(t<0)=0$, and since they are in parallel, $V_o(t<0) = 0$.
Once the switch is closed, all of the current initially starts flowing through the capacitor. Since $V_c(0^+)=V_c(0)=V_c(0^-)$, all of the voltage is across the resistor and $i_R(0^+)=\frac{25}{125}=0.2A$.

To find the equation for $i_o$, I believe I need $i_f=i_o(∞)$. However, since there isn't a resistor in parallel with the LC portion of the circuit, there is nothing to absorb the energy of the oscillating current and it appears the current through the inductor oscillates forever. So what do I put for $i_f$?

 

[berkeman]

As time goes to infinity, the capacitor is an open circuit and the inductor is a short circuit, so Vo-->0 again. The 125 Ohm resistor provides the damping for the overall circuit.

I would write the KCL for the top right node and solve the DE...

x(t)=xf+[B1cos(ωdt)+B2sin(ωdt)]e−αtx(t)=x_f+[B_1cos(ω_dt)+B_2sin(ω_dt)]e^{-αt}

What's x(t)?

 

[Drakkith]

As time goes to infinity, the capacitor is an open circuit and the inductor is a short circuit, so Vo-->0 again. The 125 Ohm resistor provides the damping for the overall circuit.

Can you elaborate? I don't understand why the resistor would provide damping to the circuit since only the inductor and capacitor are in parallel.

What's x(t)?

Insert V or i instead of x's there. It's just the general form of the formula for underdamped RLC circuits.

I would write the KCL for the top right node and solve the DE...

I'll give it a shot.

 

[Drakkith]

KCL at the top node:
$i_o+i_c=i_R$
$i_o=i_R-i_c$
To find the current, I turned everything into voltage:
$\frac{\int V_L}{L}=\frac{25-V_L}{125}-C\frac{dV_c}{dt}$
Taking the derivative gives:
$\frac{Cd^2}{dt^2}-\frac{dV}{125dt}-\frac{V}{L}=0$
Dividing by C and solving the differential equation yields:
$V_c=[B_1cos(480t)+B_2sin(480t)]e^{-640t}$

To find $B_1$ and $B_2$:
$V(0)=V(∞)+B_1$
$0=0+B_1$
$B_1=0$

$\frac{dV(0)}{dt}=-640B_1+480B_2$
$\frac{0.2}{6.25*10^{-6}}=480B_2$
$B_2=66.67$

So $V(t)=66.67sin(480t)e^{-640t}$

Plugging that back into the current equation $i_o=i_R-i_c$:
$i_o=\frac{25-V}{125}-\frac{dV}{dt}=0.2+[-0.2cos(480t)-0.267sin(480t)]e^{-640t} A$

***Interestingly, this can be converted to an RLC circuit in parallel with a 0.2 Amp current sources instead of a voltage source.

Thanks @berkeman.

 

[berkeman]

Looks pretty good to me. Are you able to check the answer?

 

[berkeman]

Can you elaborate? I don't understand why the resistor would provide damping to the circuit since only the inductor and capacitor are in parallel.

The voltage source looks like an AC short circuit (current sources are AC open circuits), so that resistor actually is in parallel with the LC in this circuit.

Also, just stepping back and looking at the circuit at t=0- and t=infinity, you can see that Vo is going to be 0V. If it were an ideal parallel LC with no loss, then yes, after you hit it with some initial energy, it will ring forever. But in this case, the source is a DC voltage source with series resistor, so as t-->infinity, the DC voltage across the ideal inductor has to go to 0V (since its resistance is zero).

Does that help?

 

[Drakkith]

The voltage source looks like an AC short circuit (current sources are AC open circuits), so that resistor actually is in parallel with the LC in this circuit.

Ah, okay. That makes sense.

Also, just stepping back and looking at the circuit at t=0- and t=infinity, you can see that Vo is going to be 0V.

Once you recognize that the circuit is a parallel RLC circuit, sure. But I didn't realize it at the time (despite the thread title suggesting otherwise). I thought I had a parallel RLC circuit that was missing its parallel resistor and happened to be in series with another resistor.

 

[donpacino]

As a follow up to what berkman said, EVERY time I analyses a circuit I do a check at DC and inf current frequency. At DC just open all the capacitors and short all the inductors, at inf do the opposite.

After you start evaluating these circuits in the frequency domain rather than the time domain (which is much easier, algebra instead of calc) you will find that this analysis will allow you to check your own work 90% of the time.