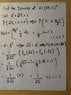Finding Density for V=(2Y1+1)^2 on U(-1,1)

  • Thread starter Thread starter James08
  • Start date Start date
  • Tags Tags
    Density
James08
Messages
2
Reaction score
0

Homework Statement



Suppose {Y1,...Yn} are random samples from U(-1,1) distribution. Find the density of V=(2Y1+1)^2

Homework Equations



Method of transformations for random variables

The Attempt at a Solution



I started this problem off by letting X=2Y1+1 because i figured i could find the density of that and then just find the density of V=X^2. I thought i had the problem right but when i went back to the density i got for X=2Y1+1 and integrated it over the interval, it didnt add up to 1. Not sure what i did wrong
 

Attachments

  • photo.JPG
    photo.JPG
    28.7 KB · Views: 383
Physics news on Phys.org
Be careful about the range of the random variable. As Y1 ranges from -1 to +1, what is the range of 2Y1+1?

RGV
 
Last edited:
Ray Vickson said:
Be careful about the range of the random variable. As Y1 ranges from -1 to +1, what is the range of 2Y1+1?

RGV

-1 to 3 right?
 

Thread 'Prove that the integral is equal to ##\pi^2/8##'

Prove $$\int\limits_0^{\sqrt2/4}\frac{1}{\sqrt{x-x^2}}\arcsin\sqrt{\frac{(x-1)\left(x-1+x\sqrt{9-16x}\right)}{1-2x}} \, \mathrm dx = \frac{\pi^2}{8}.$$ Let $$I = \int\limits_0^{\sqrt 2 / 4}\frac{1}{\sqrt{x-x^2}}\arcsin\sqrt{\frac{(x-1)\left(x-1+x\sqrt{9-16x}\right)}{1-2x}} \, \mathrm dx. \tag{1}$$ The representation integral of ##\arcsin## is $$\arcsin u = \int\limits_{0}^{1} \frac{\mathrm dt}{\sqrt{1-t^2}}, \qquad 0 \leqslant u \leqslant 1.$$ Plugging identity above into ##(1)## with ##u...
View full post »

Similar threads

Finding Probability Density Functions for Independent Random Variables
Replies
2
Views
2K
Determine marginal densities and distributions from joint density
Replies
7
Views
1K
Probability density function for a given problem
Replies
4
Views
2K
A Constructing PDFs for Max Likelihood Density Estimation Problem
Replies
2
Views
2K
Calculating the Mass of a Half Ball with Given Density δ(x, y, z)
Replies
23
Views
2K
Probability Density of ##x## (Wiener Process)
Replies
1
Views
1K
Find the density of the sum of two jointly distributed rv's
Replies
11
Views
2K
Find maximum number of ind. r.v. that follows distribution F
Replies
2
Views
1K
Find the cdf given a pdf with absolute value
Replies
3
Views
5K
N-dimensional broken stick problem -- find joint density
Replies
3
Views
950

Hot Threads

Recent Insights

Back
Top