BearMan
- 3
- 0
Just started with physics, I am not very good.
A weight with the mass m is hanging in one thread (C) that is connected to two other threads (A and B). Thread A is completely horizontal, while thread B is forming a angle of 45° with the horizontal plane. All threads are connected in the way shown in the image. The force in thread A is 15N.
My task is to figure out the force in thread B and the mass of the weight.
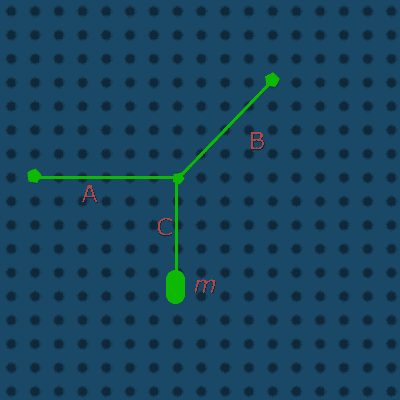
I thought that a simple use of the Pythagorean theorem would give me the power in thread B; the triangle is 4 in height, 4 in weight. The A "contains" 15N of energy and is 6 units long, therefore i divided 15 by 6 and got 2.5.
15/6=2.5
(4*2.5)^2+(4*2.5)^2=200
√(200)≈14.14N=B
That is wrong, I am sure.
I am not really sure how to solve this and I do not want the numerical answers to the questions, but rather tips and methods to solving the task.
We were not really supposed to do this perticular assignment (our teacher told us it was "stuff we had not gone through yet") but I am curious to know how one should go about solving it.
Homework Statement
A weight with the mass m is hanging in one thread (C) that is connected to two other threads (A and B). Thread A is completely horizontal, while thread B is forming a angle of 45° with the horizontal plane. All threads are connected in the way shown in the image. The force in thread A is 15N.
My task is to figure out the force in thread B and the mass of the weight.
Homework Equations
The Attempt at a Solution
I thought that a simple use of the Pythagorean theorem would give me the power in thread B; the triangle is 4 in height, 4 in weight. The A "contains" 15N of energy and is 6 units long, therefore i divided 15 by 6 and got 2.5.
15/6=2.5
(4*2.5)^2+(4*2.5)^2=200
√(200)≈14.14N=B
That is wrong, I am sure.
I am not really sure how to solve this and I do not want the numerical answers to the questions, but rather tips and methods to solving the task.
We were not really supposed to do this perticular assignment (our teacher told us it was "stuff we had not gone through yet") but I am curious to know how one should go about solving it.