Becca93
- 84
- 1
Homework Statement
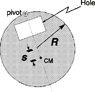
A circular disk with a rectangular hole has a radius of 0.600 m and mass of 0.390 kg. It is suspended by a point on its perimeter as shown in the figure. The moment of inertia about this point is I_p = 2.60E-1 kgm2. Its center of mass is located at a distance of s=0.120 m from the center of the circle as shown. [Photo attached]
What is the oscillation frequency if the pivot point is at the center of mass?
The attempt at a solution
In truth, there were two parts to this question. The first, I had to find the periodof oscillations if it was allowed to oscillate side to side as a pendulum.
I used the equation T = 2(pi)√(I/mgd) and found that the answer was 1.93 s.
However, I'm at a loss as to how to try to solve for the frequency with the pivot point at the center of mass. Obviously, taking the inverse of the above answer resulted in an incorrect answer.
Any and all assistance would be hugely appreciated.
A circular disk with a rectangular hole has a radius of 0.600 m and mass of 0.390 kg. It is suspended by a point on its perimeter as shown in the figure. The moment of inertia about this point is I_p = 2.60E-1 kgm2. Its center of mass is located at a distance of s=0.120 m from the center of the circle as shown. [Photo attached]
What is the oscillation frequency if the pivot point is at the center of mass?
The attempt at a solution
In truth, there were two parts to this question. The first, I had to find the periodof oscillations if it was allowed to oscillate side to side as a pendulum.
I used the equation T = 2(pi)√(I/mgd) and found that the answer was 1.93 s.
However, I'm at a loss as to how to try to solve for the frequency with the pivot point at the center of mass. Obviously, taking the inverse of the above answer resulted in an incorrect answer.
Any and all assistance would be hugely appreciated.
Attachments
Last edited: