Finding i(t) without given v(t): Solving for R in a Capacitor Circuit

[jofree87]

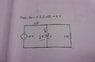
Diagram of problem attached below.

I don't know where to begin with this problem. How can I find i(t) if I am not given v(t)?

Since i = C dv/dt , don't I need the function v(t) to solve this problem?

Is it possible to use the function v(t) = v(0) e^-t/(RC) , if so, then what would the value of R be?

 

[Mindscrape]

Be a little more clear. I don't know what V you are talking about. From the voltage source you know that v(t)=3*i(t), and the voltage of the capacitor is something you need to find.

 

[jofree87]

Be a little more clear. I don't know what V you are talking about. From the voltage source you know that v(t)=3*i(t), and the voltage of the capacitor is something you need to find.

By v(t), I meant the voltage cross the capacitor, I'll just call it v_c(t). And I need to find i_c(t) which is the current through the capacitor.

I don't think the dependent source and v_c(t) are the same since they're not parallel, right?

So I need to find v_c(t) to get i_c(t). How do I find v_c(t)?

 

[Mindscrape]

You're right, the dependent voltage source and the v_c are not the same voltages.

Do you know how to do node voltage analysis, or do you know KCL?

 

[jofree87]

Here is my attempt at nodal voltage analysis attached below. Can somebody look it over? My answer doesn't seem right.

 

[Mindscrape]

Your node voltage looks great, but then you start doing some funky stuff 3/4 way down the page.

$$V=I=C\frac{dV}{dt}$$

so use separation of variables and integrate both sides to get

$$\frac{1}{C}\int_{t'=0}^{t'=t} dt' = \int_{V(0)}^{V(t)} \frac{dV}{V}$$

Then you know Vc, and use I=C dVc/dt once again to get I.

Or.. you can find I with chain rule. I=C dVc/dt = C dV/dI dI/dt. Then if Vc = I, then dVc/dI = 1, so you really get the same thing, I=C dI/dt.

You were using both I and V in your integrals, and it doesn't quite work that way.

 

[jofree87]

Your node voltage looks great, but then you start doing some funky stuff 3/4 way down the page.

$$V=I=C\frac{dV}{dt}$$

so use separation of variables and integrate both sides to get

$$\frac{1}{C}\int_{t'=0}^{t'=t} dt' = \int_{V(0)}^{V(t)} \frac{dV}{V}$$

Then you know Vc, and use I=C dVc/dt once again to get I.

Or.. you can find I with chain rule. I=C dVc/dt = C dV/dI dI/dt. Then if Vc = I, then dVc/dI = 1, so you really get the same thing, I=C dI/dt.

You were using both I and V in your integrals, and it doesn't quite work that way.

I think I am starting to get it now, but where did you get V = I in the first integral?

Thanks for helping me out btw

 

[Mindscrape]

Oh, I got the Vc=Ic from the node voltage you did (I also did up to this point to check and it was right). When everything is simplified, we get Vc=Ic. Sorry, I intermittently dropped subscripts, but all the Vs and the Is were the Vs and Is of the capacitor.