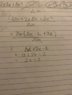Finding Limits with DeltaX: An Essential Tool for Calculus
- Thread starter Witcher
- Start date
-
- Tags
- Limit
Click For Summary
To eliminate the last delta x in calculus problems, one should take the limit as delta x approaches zero. It is essential to maintain the limit notation, lim(Δx → 0), in every step of the calculation until the limit is fully evaluated. This approach ensures that the process adheres to the principles of calculus. Properly applying limits is crucial for achieving accurate results in derivative and integral calculations. Understanding this concept is fundamental for mastering calculus techniques.
Similar threads
- · Replies 58 ·
- · Replies 4 ·
- · Replies 1 ·
- · Replies 5 ·
- · Replies 10 ·
- · Replies 5 ·
- · Replies 2 ·
- · Replies 6 ·