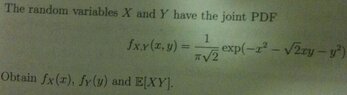nacho-man
- 166
- 0
Please see the attached image for my question. I don't understand how to compute the integral, is there some trick?
I do believe that
to find fx(x) I integrate the joint pdf, with respect to x with the bounds set as the range of Y. But this leaves me with a very complex integration
Similarly for fy(y). Is there some trick?
Any help is greatly appreciated.
I do believe that
to find fx(x) I integrate the joint pdf, with respect to x with the bounds set as the range of Y. But this leaves me with a very complex integration
Similarly for fy(y). Is there some trick?
Any help is greatly appreciated.
Attachments
Last edited by a moderator: