Finding Minimum Force Applied to Keep Objects Stationary?

AI Thread Summary
To keep the crate stationary on the incline, the minimum force F must counteract the forces acting on it, including gravitational force and friction. The coefficient of static friction is .300, and the mass of the crate is 3.00 kg with an incline angle of 35°. The equation to consider is mgsinθ - μsmgcosθ + F = 0, where F represents the additional frictional force caused by the applied force. Understanding the relationship between F and the frictional force is crucial for solving the problem. The discussion clarifies that the focus should be on how F affects the friction rather than determining F alone.
morgane28v
Messages
3
Reaction score
0

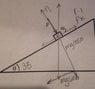
The coefficient of static friction between the crate m1=3.00kg and the incline with θ=35° shown in the figure below is .300. What minimum force F must be applied to the crate perpendicular to the incline to prevent the crate from sliding down the incline?

mgsinθ
μsmgcosθ
f=ma

I don't quite get how the applied force fits into the equation. mgsinθ-μsmgcosθ+F=0?
 

Attachments

  • phys.JPG
    phys.JPG
    19.5 KB · Views: 826
Physics news on Phys.org
Your equation is almost right. You are not interested so much in F itself but the additional frictional force caused by F.
 
Okay thank you I got it!
 

Thread 'Errors and significant figures'

I multiplied the values first without the error limit. Got 19.38. rounded it off to 2 significant figures since the given data has 2 significant figures. So = 19. For error I used the above formula. It comes out about 1.48. Now my question is. Should I write the answer as 19±1.5 (rounding 1.48 to 2 significant figures) OR should I write it as 19±1. So in short, should the error have same number of significant figures as the mean value or should it have the same number of decimal places as...
View full post »
Thread 'A cylinder connected to a hanging mass'

Thread 'A cylinder connected to a hanging mass'

Let's declare that for the cylinder, mass = M = 10 kg Radius = R = 4 m For the wall and the floor, Friction coeff = ##\mu## = 0.5 For the hanging mass, mass = m = 11 kg First, we divide the force according to their respective plane (x and y thing, correct me if I'm wrong) and according to which, cylinder or the hanging mass, they're working on. Force on the hanging mass $$mg - T = ma$$ Force(Cylinder) on y $$N_f + f_w - Mg = 0$$ Force(Cylinder) on x $$T + f_f - N_w = Ma$$ There's also...
View full post »

Similar threads

What is the minimum force required to move the box?
Replies
6
Views
4K
Minimum force required to prevent sliding down
Replies
1
Views
3K
Block at rest on an inclined surface
Replies
36
Views
5K
Push/Pull Force of wheeled cart on an incline
Replies
7
Views
4K
Help with finding Normal Force of inclined plane
Replies
1
Views
3K
What Is the Minimum Stopping Distance to Prevent Crate Sliding?
Replies
3
Views
4K
How Do You Calculate Forces on a Crate on an Inclined Plane?
Replies
5
Views
3K
Finding the force to pull a block up a frictionless slope?
Replies
12
Views
2K
How Is Normal Force Calculated on an Inclined Plane?
Replies
1
Views
2K
How is the minimum work needed to push a car up an inclined plane calculated?
Replies
4
Views
3K

Hot Threads

Recent Insights

Back
Top