- #1
Cascadian
- 6
- 0
Hi I'm trying to study over break, this isn't an exact quote but its the part of the problem I need help with. Thanks.
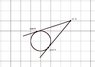
Draw the unit circle and plot the point P=(3,2). Observe there are TWO lines tangent to the circle passing through the point P. Lines L1 and L2 are tangent to the circle at what points?
I tried plugging in the point into a point-slope formula, it was kind of a dead end for me.
Homework Statement
Draw the unit circle and plot the point P=(3,2). Observe there are TWO lines tangent to the circle passing through the point P. Lines L1 and L2 are tangent to the circle at what points?
Homework Equations
The Attempt at a Solution
I tried plugging in the point into a point-slope formula, it was kind of a dead end for me.
Last edited by a moderator: