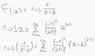Finding Residues of a Function

[asi123]

residues 2 :)

Homework Statement

Ok, so I have this function and I need to find the residues for it.
I developed the function into Laurent series and my question is, how can I find a(-1) which is the residues?

Thanks in advance.

Homework Equations

The Attempt at a Solution

 

[HallsofIvy]

The function is
f(z)= cos(\frac{1}{z-2})
and you correctly used the McLaurin series for cos(u), with u= 1/(z-2), to write the Laurent series
\sum_{n= 0}^\infty \frac{(-1)^n}{(2n)!} (z-2)^{-2n}
Since the power of z- 2 is always even, there is no (z-2)^-1 term: the coefficient is 0.

HOWEVER, because that series has an infinite number of negative powers with non-zero coefficient, z= 2 is an essential singularity, not a pole. There is NO residue.

 

[asi123]

The function is
f(z)= cos(\frac{1}{z-2})
and you correctly used the McLaurin series for cos(u), with u= 1/(z-2), to write the Laurent series
\sum_{n= 0}^\infty \frac{(-1)^n}{(2n)!} (z-2)^{-2n}
Since the power of z- 2 is always even, there is no (z-2)^-1 term: the coefficient is 0.

HOWEVER, because that series has an infinite number of negative powers with non-zero coefficient, z= 2 is an essential singularity, not a pole. There is NO residue.

Oh, so an essential singularity has no residue?

Thanks.

 

[asi123]

How about this one?

Thanks again.

 

[HallsofIvy]

The function is
f(z)= cos(\frac{1}{z-2})
and you correctly used the McLaurin series for cos(u), with u= 1/(z-2), to write the Laurent series
\sum_{n= 0}^\infty \frac{(-1)^n}{(2n)!} (z-2)^{-2n}
Since the power of z- 2 is always even, there is no (z-2)^-1 term: the coefficient is 0.

HOWEVER, because that series has an infinite number of negative powers with non-zero coefficient, z= 2 is an essential singularity, not a pole. There is NO residue.

I am informed that, according to Wikipedia, I am wrong about this. That is, that the residue is still the coefficient of the -1 power in the Laurent series. The difference is just that the formula for the residue, taking the nth derivative where n is the order of the pole, cannot be used but you still can find it by finding the Laurent series itself. In the case of your first problem, the residue is 0 and for your new problem, it is 1.