Finding resistance and capacitance

[MissP.25_5]

I am stuck, can someone help me, please? I am not sure if I started the right way, it seems tedious :(

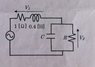
The magnitude of V1 is 2 times greater than V2, and its phase leads π/2 ahead. The angular frequency ω of the power supply voltage is 5rad/s.
Find the values of the resistance R and Capacitance C.

 

[MissP.25_5]

OK, I think I did a mistake on the impedance across the capacitor. It's a parrallel set, right?
So is this formula correct? Z2=R//(1/jwc)

So here's what I've done so far. What should I do next?

 

[MissP.25_5]

Or perhaps there is another easier way to do it?

 

[gneill]

Or perhaps there is another easier way to do it?

Perhaps there is. Rather than hammering away at the phase angles right away, remember that when you divide two complex numbers the resulting angle is the difference between the numerator's angle and the denominator's angle. So, if you divide V1/V2 you want the phase angle of the result to be $\pi/2$.

Why not suppose that the source driving the circuit is a 1A current source. Then from your work,

$V1 = 1 + 2j$

$V2 = \frac{R}{1 + 5RCj}$

Can you carry on?

(HINT: The tricky bit lies in realizing the implications of the angle being $\pi/2$)

 

[MissP.25_5]

Perhaps there is. Rather than hammering away at the phase angles right away, remember that when you divide two complex numbers the resulting angle is the difference between the numerator's angle and the denominator's angle. So, if you divide V1/V2 you want the phase angle of the result to be $\pi/2$.

Why not suppose that the source driving the circuit is a 1A current source. Then from your work,

$V1 = 1 + 2j$

$V2 = \frac{R}{1 + 5RCj}$

Can you carry on?

(HINT: The tricky bit lies in realizing the implications of the angle being $\pi/2$)

Ok, so I have to find arg(V1/V2), right? I got arg(V1/V2) = arctan((5CR+2)/(1-10R))

Am I doing this right? I want to make sure before proceeding.

 

[gneill]

Ok, so I have to find arg(V1/V2), right? I got arg(V1/V2) = arctan((5CR+2)/(1-10R))

Am I doing this right? I want to make sure before proceeding.

That's the idea. Check the denominator though, I think you've dropped a 'C'.

In order for the arctan of this expression to be $\pi/2$, what condition must hold?

 

[MissP.25_5]

That's the idea. Check the denominator though, I think you've dropped a 'C'.

In order for the arctan of this expression to be $\pi/2$, what condition must hold?

Errr...I'm guessing that the real part of the complex number aka the x-coordinate to be 0?
So, that means 1-10CR=0, and CR= 0.1 !I think that must be correct.

 

[gneill]

Errr...I'm guessing that the real part of the complex number aka the x-coordinate to be 0?
So, that means 1-10CR=0, and CR= 0.1 !I think that must be correct.

Yes, in the limit as the denominator goes to zero, the slope goes to infinity. That's the same as saying that the angle goes to vertical --- 90° or $\pi/2$ radians.

I suggest that for now you write it as $C = \frac{1}{10 R}$. (You'll see why a bit later).

Can you now use the information about the ratio of magnitudes of V1 and V2 to proceed?

 

[MissP.25_5]

Yes, in the limit as the denominator goes to zero, the slope goes to infinity. That's the same as saying that the angle goes to vertical --- 90° or $\pi/2$ radians.

I suggest that for now you write it as $C = \frac{1}{10 R}$. (You'll see why a bit later).

Can you now use the information about the ratio of magnitudes of V1 and V2 to proceed?

Yes, actually I was solving it while waiting for your reply. The answer for C is 1/25 and R is 5/2. Are my answers correct?
I can't show you my working yet because it's too messy LOL.

 

[gneill]

Yes, actually I was solving it while waiting for your reply. The answer for C is 1/25 and R is 5/2. Are my answers correct?

They're off by a factor of two. No doubt this will be discovered as you "tidy up"

I can't show you my working yet because it's too messy LOL.

Ha!

 

[MissP.25_5]

They're off by a factor of two. No doubt this will be discovered as you "tidy up"

Ha!

Yeah, I had a careless mistake there. Here it is, tell me if I did it right. You're a genius, man, thank you so much!You explain better than my own professor does, haha.

 

[gneill]

Yeah, I had a careless mistake there. Here it is, tell me if I did it right.

Looks good!

You're a genius, man, thank you so much!You explain better than my own professor does, haha.

That's very kind of you to say. Thanks!