DERC511
- 2
- 0
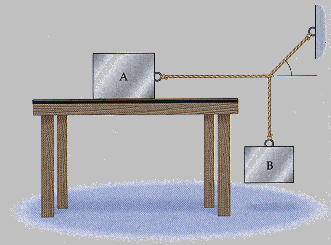
In the figure we see two blocks connected by a string and tied to a wall, with θ = 33°. The mass of the lower block is m = 0.9 kg; the mass of the upper block is 4.0 kg. Find the tension in the string that is tied to the wall.
-I have the forces of Block A as Tension, Normal Force, and Gravity (mg). From my calculations I have that Tension equals 0 (which I don't think is correct) and the Normal Force being equal to 39.2.
- For Block B I have the forces as Tension and Gravity, which gives me the Tension being equal to 8.82
- Finally,I separated the tension of the rope on the wall to the x and y components with X: Tcos33 and Y: Tsin33
- We can assume this is all in static equilibrium. Any advice on mistakes or how to proceed with this problem is much appreciated!
-I have the forces of Block A as Tension, Normal Force, and Gravity (mg). From my calculations I have that Tension equals 0 (which I don't think is correct) and the Normal Force being equal to 39.2.
- For Block B I have the forces as Tension and Gravity, which gives me the Tension being equal to 8.82
- Finally,I separated the tension of the rope on the wall to the x and y components with X: Tcos33 and Y: Tsin33
- We can assume this is all in static equilibrium. Any advice on mistakes or how to proceed with this problem is much appreciated!