Finding the Acceleration of masses on a pulley

[rodrale25]

Homework Statement

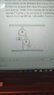
Masses M and m are connected to a system of strings and pulleys as shown
in the diagram below. The strings are massless and inextensible, and the p
ulleys are massless and
frictionless.
A: Find the accelerations for M and m (Hint: Think about these two questions:
Do these two masses have the same accelerations
in magnitude ? How is the distance that the lower pulley moves related to the distances
that masses M and m travels?)

B: One can imagine that when M is much larger than m, mass M would descend while mass m w goes up. Under what condition for M and m, would mass M go up while mass m descend? Explain your reasoning by considering the static situation (i.e., when the two masses are in equilibrium with neither M nor m moving)

Homework Equations

Sum of Forces=ma[/B]

The Attempt at a Solution

I said F= the sum of forces for just one of the masses and solved for a. Doing this for both masses, I got two separate accelerations, and then I realized that the two masses are connected. I know this isn't right because the two masses are connected by the strings somehow but I can't conceptually picture this.[/B]

 

[BvU]

Hello Rod,

I know this isn't right because the two masses are connected by the strings somehow but I can't conceptually picture this

For this reason you are given hints in the form of two questions. What are your answers?
You get a third one from me : can you imagine an equilibrium situation ? If so, under what condition ?
[edit] reading ahead can be profitable (for folks like me too ): the same question is asked in part B.