Finding the angle between two vectors

[chwala]

Homework Statement

See attached;

Relevant Equations

sine and cosine angle rules

This is clear to me; i just wanted to know in which contexts is one allowed to use one rule over the other; or it does not matter.

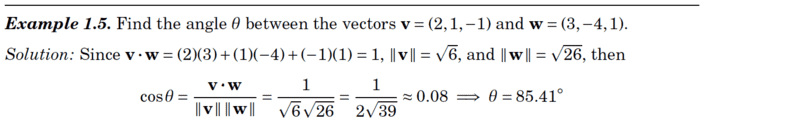
The angle i realise can also be found by;

$\sin θ = \dfrac{||v×w||}{||v||||w||}$= $\dfrac{||-3i-5j-11k||}{\sqrt{6}\sqrt{26}}$=$\dfrac{\sqrt{155}}{\sqrt{6}\sqrt{26}}=0.99679$ to 5 decimal places...

$⇒θ=\sin^{-1} [0.99679]= 85.41^0$

In which contexts is one allowed to use sine angle rule? ; or is it dependent on the question as directed? cheers...

 

[chwala]

I picked my own example as follows let;

$p=2i+3j$ and $q=3i+4j$ then;

$\cos θ= \dfrac{18}{\sqrt {13}\sqrt{25}}$

$θ = cos^{-1} [0.99846]=3.18^0$ to two decimal places

and extending it to $\mathbb{R^3}$ we shall have;

$p=2i+3j+0k$ and $q=3i+4j+0k$

on using cross product we shall end up with,

$\sin θ =\dfrac{1}{\sqrt{13}\sqrt{25}}=0.05547$ to 5 decimal places...

$⇒θ=\sin^{-1} [0.05547]= 3.18^0$

 

[anuttarasammyak]

Homework Statement:: See attached;
Relevant Equations:: sine and cosine angle rules

or it does not matter.

It does not matter. In most cases I prefer cos because I can calculate inner product easier than vector product.