supremeruler
- 10
- 0
On this triangle:
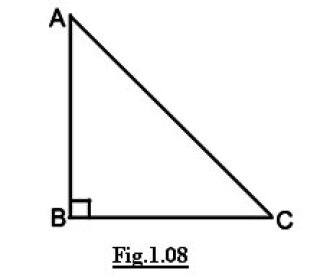
Show a formula for finding co-ordinates of B.
You know:
- the co-ordinates of A and C;
- Angle B = 90 degrees
Is this possible? If not, is it possible if you know all 3 angles?
Show a formula for finding co-ordinates of B.
You know:
- the co-ordinates of A and C;
- Angle B = 90 degrees
Is this possible? If not, is it possible if you know all 3 angles?