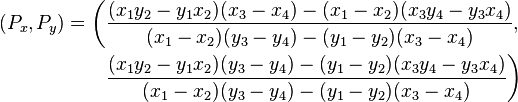Discussion Overview
The discussion revolves around finding the coordinates of the intersection point of two lines defined by four points on a plane. Participants explore various methods and formulas to determine the intersection point, including geometric approaches and algebraic formulas.
Discussion Character
- Exploratory
- Technical explanation
- Debate/contested
- Mathematical reasoning
Main Points Raised
- One participant describes the lines formed by points a, b, c, and d and seeks a formula for the intersection point e.
- Another participant suggests using midpoints for specific shapes like squares or parallelograms but acknowledges uncertainty about the correctness of this approach.
- A participant expresses the need for a formula that can determine point e, even if the coordinates are not whole numbers.
- One participant provides a formula from Wikipedia for finding the closest intersection point of multiple lines in higher dimensions, adapting it for the two lines in question.
- Another participant thanks the community for assistance but reports difficulties in applying the formula correctly.
- A later post indicates that the formula used did not yield the expected intersection coordinates, raising doubts about its applicability.
- One participant requests specific examples of lines with coordinates to demonstrate the formula's application for finding intersection points.
- Another participant shares an Excel sheet demonstrating the use of a two-dimensional formula, claiming it matches the intersection point.
- Confusion arises regarding the definitions of certain values in the formula, prompting further clarification from other participants.
- A final post indicates that the problem has been resolved, though details of the resolution are not provided.
Areas of Agreement / Disagreement
Participants express varying levels of confidence in the formulas discussed, with some agreeing on the need for clarification and others reporting difficulties in application. The discussion remains unresolved regarding the most effective method to find the intersection point, with multiple approaches and formulas being considered.
Contextual Notes
Some participants note that the formulas discussed may not apply to all scenarios, particularly regarding dimensionality and the specific geometric configuration of the lines.
Who May Find This Useful
This discussion may be useful for individuals interested in geometry, algebraic methods for finding intersections, or those seeking assistance with mathematical problem-solving in two dimensions.