- #1
Sunwoo Bae
- 60
- 4
- Homework Statement
- I am given the following matrix. I solved the question and found out that the resulting determinant is 0, thus the matrix is not invertible. However, I tried the question in another method, and I am getting a different answer for the determinant. Why is the second method not working?
- Relevant Equations
- Theorem: if a multiple of one row of A is added to another row to produce matrix B, then det B = det A
question:

My first attempt:
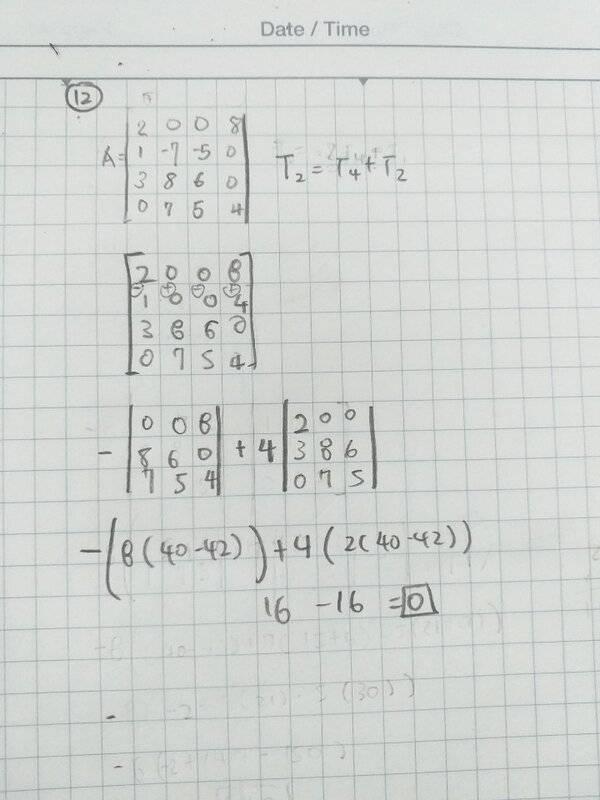
my second attempt:
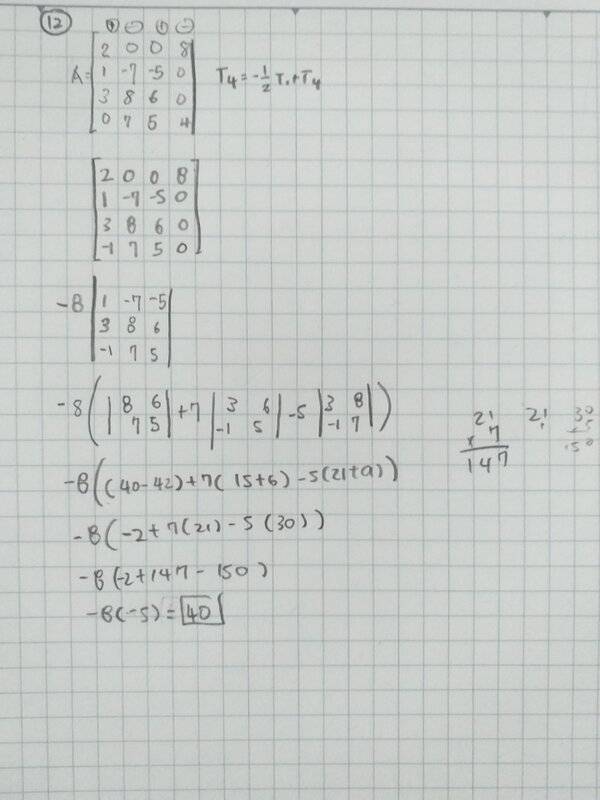 So I am getting 0 (the right answer) for the first method and 40 for the second method. According to the theorem, shouldn't the determinant of the matrix remain the same when the multiple of one row is added to another row? Can anyone explain why the second method is not working?
So I am getting 0 (the right answer) for the first method and 40 for the second method. According to the theorem, shouldn't the determinant of the matrix remain the same when the multiple of one row is added to another row? Can anyone explain why the second method is not working?
Thank you very much!
My first attempt:
my second attempt:
Thank you very much!