Finding The Distance Between An Observer and Light Source

[embphysics]

Homework Statement

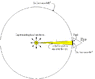
We are given that a light-bulb radiates 0.1 W from it, and the wavelength of light emitted from it is 530 nm. Seeing as the human eye requires around 6 photons per second for the brain to register a light signal. I am then asked, what is the largest possible distance between the observer and light source.

Homework Equations

The Attempt at a Solution

Well, light with a wavelength of 530 nm carries with it $E = \frac{hc}{530 \cdot 10^{-9}m}=3.747 \cdot 10^{-19} J$. Thus, $\frac{1~photon}{3.747 \cdot 10^{-19} J}$. Furthermore, the amount of the photons emitted each second in all directions is $\frac{0.1 J}{1s} \cdot \frac{1~photon}{3.747 \cdot 10^{-19} J} = 2.6688 \cdot 10^{17} \frac{photons}{s}$. This is the amount of light emitted in all directions. Let's assume there are five sides to the light source, 4 sides and 1 top. Emitting from these sides is $2.6688 \cdot 10^{17} \frac{photons}{s}$, but we can't view every side at once. So, the total amount that one can possibly see is $\frac{1}{5} (2.6688 \cdot 10^{17} \frac{photons}{s}) = 5.3376 \cdot 10^{16}$ The diameter of an average eye is 25 mm.

The distance between the eye and light source is variable. we need to find L such that only 6 photons reach the eye each second. (I would if I could use the calculus of variations somehow...)

I am not quite certain of what to do next. I have heard of some inverse square, but am not sure of how to use it.

 

[szynkasz]

Assume that light is emitted uniformly into a sphere. Its radius is the distance to observer.

 

[embphysics]

And where can I go from that assumption? Is there some sort of relationship of which is unbeknownst to me?

 

[gneill]

And where can I go from that assumption? Is there some sort of relationship of which is unbeknownst to me?

Perhaps. One also assumes that the pupil of the observing eye occupies a tiny patch of surface area on that sphere... (light enters the eye through a small opening called the pupil. You'll want to find out what the typical size is for a dilated pupil).

 

[embphysics]

gneill, I looked up the diameter of the eye and gave the value in my original post (the value being 25 mm). I was then going to use this value to find the surface area of the eye. So, are you saying that the eye only occupies a small fraction of the sphere?

 

[gneill]

gneill, I looked up the diameter of the eye and gave the value in my original post (the value being 25 mm). I was then going to use this value to find the surface area of the eye. So, are you saying that the eye only occupies a small fraction of the sphere?

Light that reaches the retina does not pass through the whole front surface of the eye -- it passes though the small opening known as the pupil. The pupil opening contracts or dilates depending upon ambient light levels. A dark adapted eye will have maximal pupil width. The maximal dilation also changes with age, with older eyes getting less flexible. The generally accepted value for an average dilated pupil is 7mm across. Optics are designed using that figure.

Yes, the cross sectional area of the observer's pupil is a small patch of area on the spherical surface. Light that passes through that small area can be detected by the eye.

 

[embphysics]

Okay, up to this point I am unsure as to how to proceed. What equation do I need? Would I need one relating how the photons spread out and the distance between the retina and light source?

 

[gneill]

Okay, up to this point I am unsure as to how to proceed. What equation do I need? Would I need one relating how the photons spread out and the distance between the retina and light source?

Yes, that's the idea. Assume that all photons are passing through the spherical surface, spread uniformly across the surface area. What fraction of the the total does the pupil's tiny area represent?

 

[embphysics]

Well, the surface area of a sphere is $4 \pi r^2$, and so isn't the eye. But all half of the spherical wavefront reaches your eye, and only half of your eye registers light. So, would it be $\frac{2 \pi r_e^2}{2 \pi r_l^2} = (\frac{r_e}{r_l})^2$. I am not sure how I would use this.

 

[embphysics]

To be honest, I truly don't know how to solve this problem. I have a vague idea of what quantities I need, and of what equations, but I am not too familiar with them, so I don't know where to start.

 

[gneill]

Think of the sphere at distance R as a Gaussian surface. All the light flux passes through that surface. The eye intercepts a tiny portion of it through its own surface area (radius r), which comprises a tiny patch of the sphere's surface.

What fraction of the total flux, or energy, or photons, does the eye catch of the total flux,..., reaching the Gaussian surface?

 

[embphysics]

Oh, okay. So, can we assume that the photons are uniformly distributed on the surface of the spherical wavefront? And the total number of photons emitted each second is 2.6688⋅10^17, so would $\frac{2.6688⋅10^{17}}{4 \pi r^2}$ represent the amount of photons per unit area? And as r increases, that is, the spherical wavefront moves further from the light source, the density decrease because the photon spread out?

 

[gneill]

Oh, okay. So, can we assume that the photons are uniformly distributed on the surface of the spherical wavefront? And the total number of photons emitted each second is 2.6688⋅10^17, so would $\frac{2.6688⋅10^{17}}{4 \pi r^2}$ represent the amount of photons per unit area? And as r increases, that is, the spherical wavefront moves further from the light source, the density decrease because the photon spread out?

That's the idea. If the total particle flux is $\Phi = 2.6688⋅10^{17}$ / second reaching the Gaussian surface of radius R, then what fraction passes through an aperture cut into its surface with the area of the eye's pupil (radius small r)?

 

[embphysics]

So, $\frac{2.6688⋅10^{17}}{4 \pi r^2}$ can be thought of our photon density. We want to solve for this when the the photon density is 6 photons reaching your eye each second.

$\frac{2.6688⋅10^{17}}{4 \pi r^2} \cdot (4 \pi \cdot 7 \cdot 10^{-3}) = 6$ (On the LHS of the equation, the second term in the product is the surface area of the retina) So, would solving for r give me the maximum distance between the light source and observer?

 

[gneill]

That's the idea. You want to use the radius of the pupil in its area expression, and be sure to square it. Area has units of square meters. Symbolically, if R is the radius of the sphere and r the radius of the pupil, and if $\Phi$ is the total flux reaching the sphere (in particles per second), then the portion that enters the eye is:
$$\phi = \frac{4 \pi r^2}{4 \pi R^2} \Phi$$

The ratio of the areas is the ratio of the fluxes. Simplify and find R that meets your criterion.