Finding The Effect of Several Electrics Fields

  • Thread starter Thread starter Bashyboy
  • Start date Start date
  • Tags Tags
    Fields
Join the discussion
Registration is free. Ask a follow-up in this thread, or start your own.
Sign up Log in
9 replies · 1K views
Bashyboy
Messages
1,419
Reaction score
5

Homework Statement


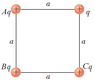
Four charged particles are at the corners of a square of side a as shown in the figure below. (Let A = 5, B = 2, and C = 7.)


Homework Equations





The Attempt at a Solution


Well, I first found the electric due to each particle individually:

[itex]\vec{E_A}=k_e\frac{5q}{a^2}\widehat{i}[/itex]

[itex]\vec{E_B}=k_e \large[ \frac{2q~cos(45°)}{a^2}\widehat{i}+\frac{2q~sin(45°)}{a^2}\widehat{j}][/itex]

[itex]\vec{E_C}=k_e\frac{7q}{a^2}\widehat{j}[/itex]

Summing the effects of the each electric field together:

[itex]\vec{E_{tot}}=k_e \large[(\frac{5q+2q\cos{45°}}{a^2}\widehat{i}+(\frac{2q \sin{45°}+7q}{a^2}\widehat{j}[/itex]

After simplifying, I found the magnitude of the electric field at point q, that the three particles create, to be [itex]10.58 \cdot \frac{q}{a^2}[/itex]; however, the true answer is, [itex]9.59 \cdot \frac{q}{a^2}[/itex] What did I do wrong?
 

Attachments

  • 23-p-025-alt.gif
    23-p-025-alt.gif
    2.9 KB · Views: 441
Last edited:
Physics news on Phys.org
You did not include a diagram or describe what you are asked to find.
 
Sorry. I just attached one.
 
Wouldn't it be [itex]\sqrt{2}a[/itex]?
 
I figured it would be better to resolve the electric field of B into its components.
 
Bashyboy said:
Wouldn't it be [itex]\sqrt{2}a[/itex]?
Right.
Bashyboy said:
I figured it would be better to resolve the electric field of B into its components.
Nothing wrong with that, but you must use the correct distance to calculate the field.
 
Well, to get from point B to point q, don't I have to go a units to right and a units north? What are the correct distances?
 
Bashyboy said:
Well, to get from point B to point q, don't I have to go a units to right and a units north? What are the correct distances?
You just gave the correct distance in your earlier post. Use it!
 
Oh I see, I am mixing the idea of resolving charges and distances together.