Finding the launch velocity of a point charge in a e-field

[jisbon]

Homework Statement

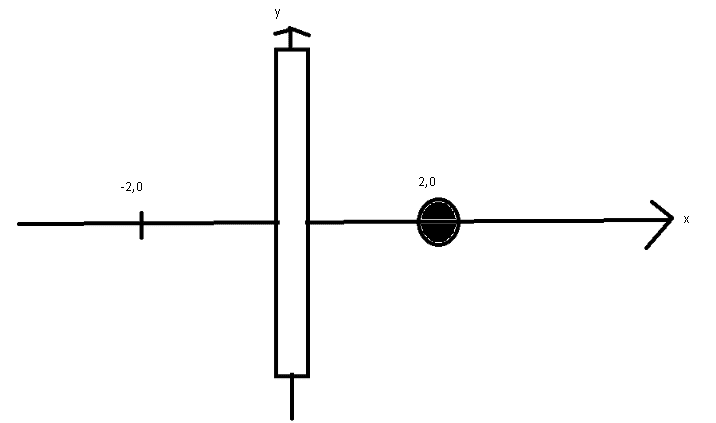
Consider a long line of charge with linear charge density λ=4μC/m
There is a point charge mass 0.1kg, q= −2μC at coordinate (-2,0) at t=0.
A point charge is then launched into the paper.
What is the launch velocity so point charge can reach coordinate (-2,0)?

Relevant Equations

$E=\frac{\lambda}{2\pi r\epsilon_{0}}$
$a= \frac{\epsilon_{0} q}{m}$

I'm not sure how to proceed with this, but here are my findings/hypothesis:

First we find the electric field contributed by the plate with $E=\frac{\lambda}{2\pi r\epsilon_{0}}$ where r=2?

After finding out the electric field, is it safe to assume I can find the acceleration of the point charge using $a= \frac{\epsilon_{0} q}{m}$? What do I do to the charge of the particle then? Am I calculating the wrong thing? Should I instead be calculating something else?

After finding out the acceleration, I am then supposed to find the initial velocity, which can be explained using kinematics equation am I right?

Please advice. Thank you.

Diagram as follows:

 

[Delta2]

I fail to understand the statement of the problem even though a figure is provided (and if it wasn't that I wouldn't understand a simple thing, lol)

Is there a point charge at (-2,0) and we want to find with what velocity(I suppose the minimum) we have to launch another point charge from 2,0 so that it reaches the point charge located at -2,0?

OR

The minimum launch velocity of the point charge at -2,0 such that it reaches point 2,0 (assume it can pass through the linear charge density at the y axis)?

OR something else which I don't understand?

 

[TSny]

I think there is only one point charge. It is given an initial velocity directed perpendicular to the plane of the drawing.

 

[Delta2]

Thanks @TSny now it all makes sense.

 

[Delta2]

The key thing to understand here is that the acceleration of the E-field is in the radial direction and it can act as centripetal acceleration for circular motion (with the plane of the circular motion perpendicular to y-axis).

You are doing fine calculating the E-field at r=2 and the acceleration at r=2.

What must be the magnitude of the initial velocity such that the acceleration acts as centripetal acceleration?

 

[TSny]

After finding out the electric field, is it safe to assume I can find the acceleration of the point charge using $a= \frac{\epsilon_{0} q}{m}$?

In this equation for the acceleration, the $\epsilon_0$ should be replaced by what quantity?

 

[jisbon]

I think there is only one point charge. It is given an initial velocity directed perpendicular to the plane of the drawing.

Yep, thanks for explaining :)

The key thing to understand here is that the acceleration of the E-field is in the radial direction and it can act as centripetal acceleration for circular motion (with the plane of the circular motion perpendicular to y-axis).

You are doing fine calculating the E-field at r=2 and the acceleration at r=2.

What must be the magnitude of the initial velocity such that the acceleration acts as centripetal acceleration?

Pardon me, but when you mean circular I suppose it's something like this?
**SIDE VIEW** (Since the charge is launched into the plane)

$E=\frac{\lambda}{2\pi r\epsilon_{0}} = \frac{4*10^{-6}}{2\pi(2)(8.85*10^{-12})} = 35967.2187$
$a= \frac{E q}{m} = \frac{(35967.2187) (-2*10^{-6})}{0.1} = -0.719344374$
$a= \frac{v^2}{r}$
$v = 1.20m/s$

Woops, I got it haha. Thanks so much :D

In this equation for the acceleration, the $\epsilon_0$ should be replaced by what quantity?

Oh that was a typo, supposed to be E. My bad :/

 

[haruspex]

Pardon me, but when you mean circular I suppose it's something like this?
**SIDE VIEW** (Since the charge is launched into the plane)
View attachment 249994

I think you still do not have the right picture.
Change the rectangle to a dot, representing a line of charge normal to the plane of your drawing, and make the trajectory semicircular.