appletree23
- 12
- 2
I'm given this code to plot the system for task 1 where my teacher have used some random numbers just to show us how the code can be used:

The code makes a plot that is given below:
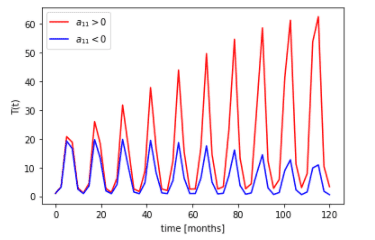
So my professor just gave us this code and plot without saying anything more. All the students in the class have also been given a set of unique coefficients in a table for a11, a12, a21,a22, forcing and amplitude and period for the second cycle it says. We are supposed to use this code above to solve a-c. What I don't understand is the line:
dT/dt=( a11+Temperature_Cycles(t, 0.35, 1)+Temperature_Cycles(t, 0.5, 1.5) )*T+forcing
I guess in a and b I set forcing=0 since they don't ask about adding forcing. But when making an annual cycle, should I just get rid of one of the Temperature_Cycles () in the line above? And when plotting the systems with two cycles, I must keep both Temperature_Cycles expressions?
I also struggle with understanding problem number 2:

I don’t understand if I should use the values a11=a12=a21=1 or my own unique value given from the table in both task 2a and 2b because it says table in the text above in brackets after the task defines the values. How do you guys interpret this?
This is the code (down below) we are supposed to use to solve task 2 by the way if someone wonder. And my teacher says we are only supposed to change the values in matrix except from a22.
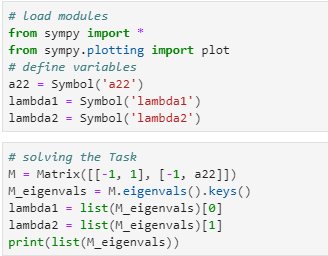
The code makes a plot that is given below:
So my professor just gave us this code and plot without saying anything more. All the students in the class have also been given a set of unique coefficients in a table for a11, a12, a21,a22, forcing and amplitude and period for the second cycle it says. We are supposed to use this code above to solve a-c. What I don't understand is the line:
dT/dt=( a11+Temperature_Cycles(t, 0.35, 1)+Temperature_Cycles(t, 0.5, 1.5) )*T+forcing
I guess in a and b I set forcing=0 since they don't ask about adding forcing. But when making an annual cycle, should I just get rid of one of the Temperature_Cycles () in the line above? And when plotting the systems with two cycles, I must keep both Temperature_Cycles expressions?
I also struggle with understanding problem number 2:
I don’t understand if I should use the values a11=a12=a21=1 or my own unique value given from the table in both task 2a and 2b because it says table in the text above in brackets after the task defines the values. How do you guys interpret this?
This is the code (down below) we are supposed to use to solve task 2 by the way if someone wonder. And my teacher says we are only supposed to change the values in matrix except from a22.