- #1
carrotstien
- 28
- 0
I am trying to write a simulation program for a relatively complicated mechanical system. Parts of it will be strings wrapped around discs under tension - with the discs moving and rotating. So, I decided to figure out the basics, and am stuck.
The situation is thus:
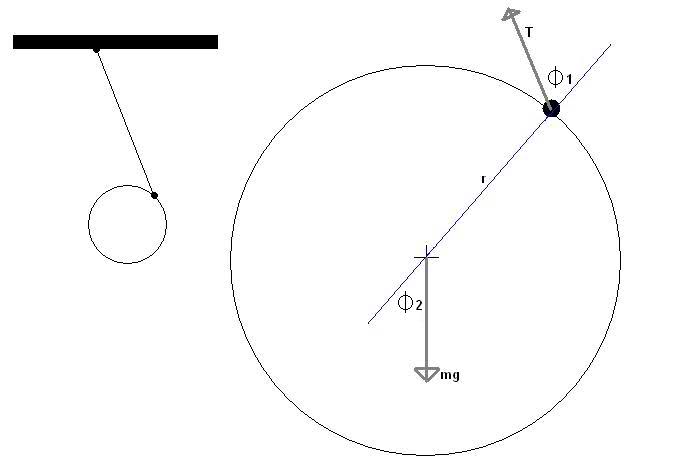
An unstretchable string is attached to a point on a ceiling. The other end, is attached at some point on the circumference of a disc. The disc is rotated and moved to some position, and then let go. How it is rotated, and moved, would determine the exact point at which the string pulls on the disc. Assuming that I know the velocities (linear and angular), and the positions and angles of the disc and string-effect-on-disc points, how would I determine the tension in the string when the disc is let go?
Or, simpler - if you glue a string to the edge of a quarter, and attach the other end to the ceiling, move the quarter to the side a bit, and rotate it at some angle - the moment when you let go of the quarter, what is the tension in the string?
I have figured out / stated a bunch of stuff below..still stuck
\ddot{X} = \frac{m\vec{g}+\vec{T}}{m}
\ddot{\theta}_{cm}I_{cm} = (\vec{R}\times\vec{T})_{k}
from here, I had three unknowns and two equations.
I tried using conservation of energy, but that got me no where:
E_{initial}=E_{final}
0=\frac{dE}{dt}=(\frac{dKE_{linear}}{dt}) + (\frac{dKE_{angular}}{dt}) + (\frac{dPE_{gravitational}}{dt})
0=(m\dot{X}\cdot\ddot{X}) + (I_{cm}\dot{\theta}_{cm}\ddot{\theta}_{cm}) + (mg\dot{X}_{j})
and plugging in the first two formulas into the last...
0=(\dot{X}\cdot({m\vec{g}+\vec{T}})) + (\dot{\theta}_{cm}(\vec{R}\times\vec{T})_{k}) + (mg\dot{X}_{j})
unfortunately...
0=(-mg\dot{X}_{j}+\dot{X}\cdot \vec{T}) + (\dot{\theta}_{cm}(\vec{R}\times\vec{T})_{k}) + (mg\dot{X}_{j})
which means
0=(\dot{X}\cdot \vec{T}) + (\dot{\theta}_{cm}(\vec{R}\times\vec{T})_{k})
however, this tells me nothing about T, since every T solves the equation
interestingly, this equation just shows the relationship between angular velocity and linear velocity - neato...but currently useless.
So after making a nice head-shaped indent in the wall of my room, I decided to just look at it from a different perspective.
Instead of taking the point of rotation to be the center of the disc, I decided to take it as the point at which the string is acting on the disc (this would be the point of attachment, unless the string is wrapped around, and then it would be a tangential point...but that is irrelevant)
from the attached picture...
\ddot{\theta}_{cm} = \frac{(\vec{R}\times\vec{T})_{k}}{I_{cm}}
converting to scalar notation, where T is the tension in the string
\ddot{\theta}_{cm} =\frac{ rTsin({\phi}_{1})}{I_{cm}}
similarly cn = 'connection point on disc or point at which the string is acting on the disc'
\ddot{\theta}_{cn} =\frac{ (rmg)sin({\phi}_{2})}{I_{cn}}
Now, this may be a wrong assumption, but it seems valid in my mind for several reasons, but..I assumed that
\ddot{\theta}_{cm} = \ddot{\theta}_{cn}
if this is true, then
\frac{ rTsin({\phi}_{1})}{I_{cm}} = \frac{ (rmg)sin({\phi}_{2})}{I_{cn}}
which would mean that
T = \frac{I_{cm}}{I_{cn}}\frac{sin({\phi}_{2})}{sin({\phi}_{1})}mg
moment of inertia:
I_{cm} = \frac{mr^{2}}{2}
parallel axis theorum
I_{cn} = I_{cm} + mr^{2}
I_{cn} = \frac{3mr^{2}}{2}
and
\frac{I_{cm}}{I_{cn}} = \frac{1}{3}
which leaves
T = \frac{1}{3}\frac{sin({\phi}_{2})}{sin({\phi}_{1})}mg
which seems fine and dandy until you look at what happens when both angles are very very small...u get a 0/0...and both num and den can approach 0 at the same rate (in some particular case)
which would mean that, in the limit as the angles approach 0, in that particular case ^
T = \frac{mg}{3}
even though T should equal mg for all cases when the angles approach 0.
did I just screw up somewhere?...or is my last limiting argument incorrect?
And, if I didn't get near the answer...how would you determine the tension?
...
if you got to this point..thanks for reading this whole giant post :)
The situation is thus:
An unstretchable string is attached to a point on a ceiling. The other end, is attached at some point on the circumference of a disc. The disc is rotated and moved to some position, and then let go. How it is rotated, and moved, would determine the exact point at which the string pulls on the disc. Assuming that I know the velocities (linear and angular), and the positions and angles of the disc and string-effect-on-disc points, how would I determine the tension in the string when the disc is let go?
Or, simpler - if you glue a string to the edge of a quarter, and attach the other end to the ceiling, move the quarter to the side a bit, and rotate it at some angle - the moment when you let go of the quarter, what is the tension in the string?
I have figured out / stated a bunch of stuff below..still stuck
\ddot{X} = \frac{m\vec{g}+\vec{T}}{m}
\ddot{\theta}_{cm}I_{cm} = (\vec{R}\times\vec{T})_{k}
from here, I had three unknowns and two equations.
I tried using conservation of energy, but that got me no where:
E_{initial}=E_{final}
0=\frac{dE}{dt}=(\frac{dKE_{linear}}{dt}) + (\frac{dKE_{angular}}{dt}) + (\frac{dPE_{gravitational}}{dt})
0=(m\dot{X}\cdot\ddot{X}) + (I_{cm}\dot{\theta}_{cm}\ddot{\theta}_{cm}) + (mg\dot{X}_{j})
and plugging in the first two formulas into the last...
0=(\dot{X}\cdot({m\vec{g}+\vec{T}})) + (\dot{\theta}_{cm}(\vec{R}\times\vec{T})_{k}) + (mg\dot{X}_{j})
unfortunately...
0=(-mg\dot{X}_{j}+\dot{X}\cdot \vec{T}) + (\dot{\theta}_{cm}(\vec{R}\times\vec{T})_{k}) + (mg\dot{X}_{j})
which means
0=(\dot{X}\cdot \vec{T}) + (\dot{\theta}_{cm}(\vec{R}\times\vec{T})_{k})
however, this tells me nothing about T, since every T solves the equation
interestingly, this equation just shows the relationship between angular velocity and linear velocity - neato...but currently useless.
So after making a nice head-shaped indent in the wall of my room, I decided to just look at it from a different perspective.
Instead of taking the point of rotation to be the center of the disc, I decided to take it as the point at which the string is acting on the disc (this would be the point of attachment, unless the string is wrapped around, and then it would be a tangential point...but that is irrelevant)
from the attached picture...
\ddot{\theta}_{cm} = \frac{(\vec{R}\times\vec{T})_{k}}{I_{cm}}
converting to scalar notation, where T is the tension in the string
\ddot{\theta}_{cm} =\frac{ rTsin({\phi}_{1})}{I_{cm}}
similarly cn = 'connection point on disc or point at which the string is acting on the disc'
\ddot{\theta}_{cn} =\frac{ (rmg)sin({\phi}_{2})}{I_{cn}}
Now, this may be a wrong assumption, but it seems valid in my mind for several reasons, but..I assumed that
\ddot{\theta}_{cm} = \ddot{\theta}_{cn}
if this is true, then
\frac{ rTsin({\phi}_{1})}{I_{cm}} = \frac{ (rmg)sin({\phi}_{2})}{I_{cn}}
which would mean that
T = \frac{I_{cm}}{I_{cn}}\frac{sin({\phi}_{2})}{sin({\phi}_{1})}mg
moment of inertia:
I_{cm} = \frac{mr^{2}}{2}
parallel axis theorum
I_{cn} = I_{cm} + mr^{2}
I_{cn} = \frac{3mr^{2}}{2}
and
\frac{I_{cm}}{I_{cn}} = \frac{1}{3}
which leaves
T = \frac{1}{3}\frac{sin({\phi}_{2})}{sin({\phi}_{1})}mg
which seems fine and dandy until you look at what happens when both angles are very very small...u get a 0/0...and both num and den can approach 0 at the same rate (in some particular case)
which would mean that, in the limit as the angles approach 0, in that particular case ^
T = \frac{mg}{3}
even though T should equal mg for all cases when the angles approach 0.
did I just screw up somewhere?...or is my last limiting argument incorrect?
And, if I didn't get near the answer...how would you determine the tension?
...
if you got to this point..thanks for reading this whole giant post :)
