Time Average Value of Pendulum String Tension

[alan123hk]

I have a thought in my mind, that is, when the initial angle is greater than 90 degrees, whether the average tension will always be less than 1mg. After some effort, if there is no error in my calculation, I finally found that for example, the initial angle is 175 degrees, the average tension will be much less than 1mg. I believe that when the angle is closer to 180 degrees, the average tension may even gradually approach zero.

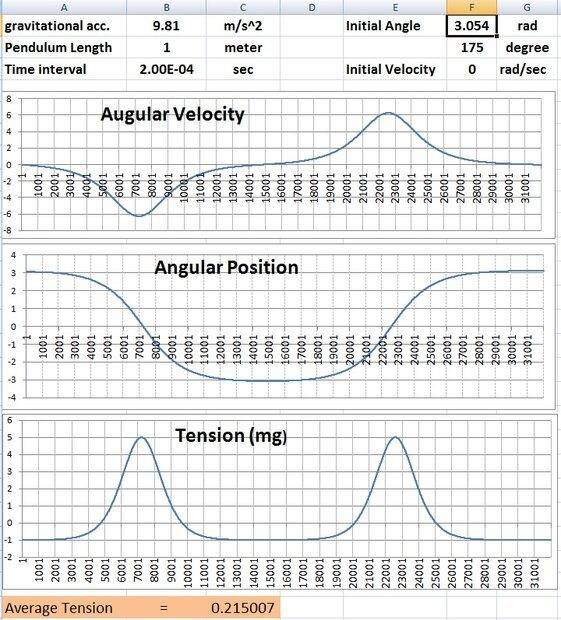
By the way, I am considering the practical application of the calculation of this tension time average. One of the possible applications is that the probability of deformation and breaking or the service life of the rigid inflexible rod of the pendulum is proportional to the average tension. But I don't know if I should use the time average of absolute values in this case.

 

[cmb]

Isn’t it obvious that the mean force has to be mg or 1. The string would have to be changing length or 2. The suspension point would have to be moving.
If not, I think we could be into a reactionless drive system.

Vertically yes, that was my point.

But in the horizontal there has to be a

 

[cmb]

Let me please ask a different question that might hold the same answer: Let's consider increasing the angular displacement of the pendulum in our calculation until it approaches pi (we can also consider exceeding pi?);-

Let's assume the pendulum is a stiff inflexible rod of negligible mass.

At some operational point as the pendulum motion approaches pi, the tension in the rod will go to zero at some point on the upward swing and reverse to compression, according to the mass of the pendulum bob, m.

As it just reaches the top of the swing and increasingly balances before going 'over the top', the 'time average' tension will clearly approach negative mg, -mg, because it may balance for a long time at the top of the swing. It spends longer at high angular displacements than at small ones.

Ergo, if the force is time averaged (by dt), it is probably a lower average tension generally, and will tend to zero and even negative (compression) in some conditions (imagine it balances exceeedingly close to pi for a long time before swinging back). If it is averaged according to angle, a (i.e. averaged by da), it will clearly be a completely different answer.

I would argue, independent of maths, the thought experiment above suggests the angle of excursion of the pendulum clearly makes a difference to the answer, and deciding what you are integrating the tension against (angle or time) likewise requires resolution before there is any satisfactory answer.

 

[Office_Shredder]

Yes as mentioned in #6 to be sure we were on the same page:
Is there an easy (not involving looking up elliptic functions although that was well done) to answer the original question About time average of T definitively (is it greater than mg) ? Something involving the triangle inequality and positive definiteness? I can't seem to pin it down, and it is niggling at me.

If $T_x(t)$ is the tension in the x direction at time t, and similar for $T_y(t)$, and one full period has time $p$, then the average tension is

$$\frac{1}{p} \int_0^p \sqrt{T_x^2+T_y^2} dt > \frac{1}{p} \int_0^p \sqrt{T_y^2} dt = \frac{1}{p} \int_0^p |T_y| dt \geq mg$$

The first strict inequality comes from the fact that $T_x$ is almost everywhere non-zero, and the second inequality comes from the fact that the signed average y tension is mg, so if e.g. the pendulum does full rotations you might get a strict inequality.

 

[hutchphd]

Ty(t), and one full period has time p, then the average tension is

Yes that looks fine. I am more a trifle chagrinned that I couldn't seem to write it down! Thanks.