Finding the work done by a Stirling Cycle

[TheBigDig]

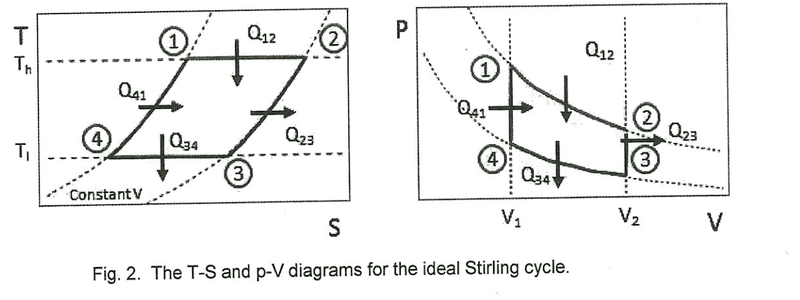
1. Given the following p-V diagram of an ideal Stirling Cycle, determine the theoretical values of W₁₂, Q₁₂, W₃₄ and Q₃₄ in terms of T₁, T₂, V₁, V₂, n (the number of moles) and R (the universal gas constant). Determine the total theoretical p-V work W₁₂₃₄₁ for the full cycle.2. dU = dQ-Pdv3. I've only just started thermodynamics recently, so my grasp on it is still very weak. I've tried finding W₁₂ using W = -∫pdV but I'm not really sure how that gives me theoretical work. I think I'm supposed to end up with some sort of numerical answer for the final part to compare it with an actual p-V work value and find the efficiency of the Stirling Engine.

 

[kuruman]

I've tried finding W₁₂ using W = -∫pdV but I'm not really sure how that gives me theoretical work.

When you write W₁₂ = - ∫p dV, both p and V are changing from 1 to 2. How about replacing p with something else using the ideal gas law?

 

[Nidum]

The working fluid in an ideal Stirling cycle engine goes through four processes :

Compression at constant temperature .
Heat addition at constant volume .
Expansion at constant temperature .
Heat removal at constant volume .

Can you identify the four processes on your diagrams ?

What formulas apply to each process ?

Reading material :

Stirling Cycle
Constant temperature process
Constant volume process

 

[TheBigDig]

The working fluid in an ideal Stirling cycle engine goes through four processes :

Compression at constant temperature .
Heat addition at constant volume .
Expansion at constant temperature .
Heat removal at constant volume .

Can you identify the four processes on your diagrams ?

What formulas apply to each process ?

Reading material :

Stirling Cycle
Constant temperature process
Constant volume process

Oh thank you! Your response was very illuminating. I hope you don't mind but I'd just like to check I've got this right:
For Isothermal Expansion : W = nRTln[V_f/V_i]
For Isothermal Compression: W = - nRTln[V_f/V_i]
For Heat Addition: Q = nC_vΔT
For Heat Removal: Q = - nC_vΔT