- #1
Est120
- 51
- 3
- Homework Statement
- Expression for "Work" in thermodynamics
- Relevant Equations
- Newton's 2nd law, ideal gas equation of state
i can't manage to grasp the concept of PV work in thermodynamics, for example we all know that W= integral(F*dx) like here

but this says that, at the end, W doesn't really depend on the gas temperature or reversible process crap
at the end W is simply a constant, atmospheric pressure is constant, piston weight is constant (and since V2=V1=0, and we neglect friction)
so that's absolutely understandable for me but in thermodynamics books:
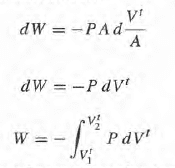
and this doesn't agree with the first equation because here we need to have a reversible process in such a way that we can always associate a definite value for P to the gas
there is absolutely NO book that explains PV work in an understandable way , in thermodynamics work isn't just "Force x distance"
but this says that, at the end, W doesn't really depend on the gas temperature or reversible process crap
at the end W is simply a constant, atmospheric pressure is constant, piston weight is constant (and since V2=V1=0, and we neglect friction)
so that's absolutely understandable for me but in thermodynamics books:
and this doesn't agree with the first equation because here we need to have a reversible process in such a way that we can always associate a definite value for P to the gas
there is absolutely NO book that explains PV work in an understandable way , in thermodynamics work isn't just "Force x distance"