Finding the work done by Spiderman

[haruspex]

Thank you for your reply @haruspex!

r is the radius to where the rope hangs from so is the length of the rope
$\theta$ is the angle the rope makes with the vertical

Many thanks!

So r is a constant, but you integrate wrt it?

 

[member 731016]

So r is a constant, but you integrate wrt it?

Thank you for your reply @haruspex!

I think take it out of the work integral that will wrt to theta

Many thanks!

 

[haruspex]

Thank you for your reply @haruspex!

I think take it out of the work integral that will wrt to theta

Many thanks!

Right.
Don't just throw integrals together that seem to have the right ingredients. Think what the integral is saying.
In the present case, you are considering spiderman moving as the rope swings, so the independent variable is the angle. As it swings through a small angle $d\theta$, Spiderman moves a distance (what?) at an angle (what?) to the vertical force (what?) thereby doing work (what?).

 

[member 731016]

Right.
Don't just throw integrals together that seem to have the right ingredients. Think what the integral is saying.
In the present case, you are considering spiderman moving as the rope swings, so the independent variable is the angle. As it swings through a small angle $d\theta$, Spiderman moves a distance (what?) at an angle (what?) to the vertical force (what?) thereby doing work (what?).

Thank you for your reply @haruspex ! That is good advice! I have tried to include my reasoning below.

Since we know that the when the spider man moves an infinitesimal displacement $\vec {ds} = dx\hat i + dy\hat y$ when a $F_g$ is applied by the earth

$dW = F_g \cdot \vec {ds}$

We know the path spider man travels though is a circular arc of length $S = r\theta$ (The arc length is dependent of the theta)

Given that the arc length of the path is $S = r\theta$, we take the derivative of arc length with respect to theta giving $ds = r\theta d\theta$

$dW = Fr\cos\theta d\theta$ Where $d\theta$ is the angle between the weight and displacement vector $\vec ds$ tangent to the circular path at each point

Ok so know we need to get $\cos\theta$ in terms of the angle the rope makes with the vertical $\phi$ (I just defined that variable)

However, do you please know how do you do that?

I think maybe from geometry (if I proved it correctly) $\theta = \phi$

Many thanks!

 

[haruspex]

the angle the rope makes with the vertical ϕ (I just defined that variable)

When you wrote S=rθ, weren’t you taking θ to be that variable?

 

[member 731016]

When you wrote S=rθ, weren’t you taking θ to be that variable?

Thank you for your reply @haruspex !

I think I changed the variables. I now take $\phi$ as the angle between the vertical and the rope and $d\theta$ as the angle between the force of gravity and differential displacement $\vec {ds}$

Many thanks!

 

[haruspex]

I think I changed the variables. I now take $\phi$ as the angle between the vertical and the rope and $d\theta$ as the angle between the force of gravity and differential displacement $\vec {ds}$

Then this is wrong:

Given that the arc length of the path is $S = r\theta$, we take the derivative of arc length with respect to theta giving $ds = r\theta d\theta$

$dW = Fr\cos\theta d\theta$ Where $d\theta$ is the angle between the weight and displacement vector $\vec ds$ tangent to the circular path at each point

Please update those equations using your new definitions.

Edit: just noticed your step from $S = r\theta$ to $ds = r\theta d\theta$ is also wrong.

 

[member 731016]

Then this is wrong:

Please update those equations using your new definitions.

Edit: just noticed your step from $S = r\theta$ to $ds = r\theta d\theta$ is also wrong.

Thank you for your reply @haruspex!

I see my mistake, it should be $ds = rd\theta$

I will post the update equations soon.

Many thanks!

 

[member 731016]

Here are the new equations @haruspex ,

We start with $dW = Fr\cos\theta d\theta$

And we must integrate from $\phi_1$ to $\phi_2$ so $dW = \int_{\phi_1}^{\phi_2} Fr\cos\theta d\theta$

Therefore, since $\theta$ depends on $\phi$ we must get $\theta$ in terms of $\phi$. I did this geometrically and proved that $\theta = \phi$.

Am I correct?

Many thanks!

 

[haruspex]

Here are the new equations @haruspex ,

We start with $dW = Fr\cos\theta d\theta$

And we must integrate from $\phi_1$ to $\phi_2$ so $dW = \int_{\phi_1}^{\phi_2} Fr\cos\theta d\theta$

Therefore, since $\theta$ depends on $\phi$ we must get $\theta$ in terms of $\phi$. I did this geometrically and proved that $\theta = \phi$.

Am I correct?

Many thanks!

If ϕ is the angle between the vertical and the rope then S=rφ.
When ϕ=0, what is the angle between $\vec ds$ and the gravitational force?

 

[member 731016]

If ϕ is the angle between the vertical and the rope then S=rφ.
When ϕ=0, what is the angle between $\vec ds$ and the gravitational force?

Thank you for your reply @haruspex !

True I did not realize that s =rφ.

I should then take the of the new arc length equation with respect to phi to get $\frac{ds}{d\phi} = r$

When $\phi$ is zero, then $\theta$ the angle between $\vec {ds}$ and $F_g$ is 90 degrees.

Are you trying to get me to find the relationship between $\phi$ and $\theta$ by considering a few physical situations?

If I consider the second case where $\phi$ is 90 degrees, then the angle between $\vec {ds}$ and $F_g$ is 180 degrees, correct?

Is there a way to find the relationship between $\phi$ and $\theta$ without considering intuitive cases along the circular path?

Many thanks!

 

[haruspex]

Is there a way to find the relationship between ϕ and θ without considering intuitive cases along the circular path?

Of course: draw the right diagram. The special cases are just an easy way to check your answer.
If you thought you had proved a different relationship, try to see where that proof went wrong.

 

[member 731016]

Of course: draw the right diagram. The special cases are just an easy way to check your answer.
If you thought you had proved a different relationship, try to see where that proof went wrong.

Thank you for your reply @haruspex !

Based on my special cases in post #81,

1. $\phi = 0$ then $\theta = 90$

2. $\phi = 90$ then $\theta = 180$

It looks to me like the relationship is $\theta = \phi+ 90$ so theta is always a phase shift of 90 degrees ahead of phi.

I will draw a diagram again to prove this and post it soon!

Many thanks!

 

[member 731016]

Here is are my diagrams @haruspex

Could you please give me some more guidance, I am still getting $\theta = \phi$

But I guess I'm meant to be looking at differential displacement so I can see here that $\theta = 180$

many thanks!

 

[haruspex]

Here is are my diagrams @haruspex
View attachment 322556
View attachment 322558

Could you please give me some more guidance, I am still getting $\theta = \phi$

But I guess I'm meant to be looking at differential displacement so I can see here that $\theta = 180$
View attachment 322560
many thanks!

You have drawn $\theta$ as the angle the final displacement makes to the vertical. You defined it as the angle the displacement element $\vec ds$ makes to the vertical at an intermediate point.
Draw a diagram with the rope at two angles to the vertical, $\phi$ and $\phi+d\phi$.
The displacement element is length $r.d\phi$. Note that it is at right angles to the rope.

 

[member 731016]

You have drawn $\theta$ as the angle the final displacement makes to the vertical. You defined it as the angle the displacement element $\vec ds$ makes to the vertical at an intermediate point.
Draw a diagram with the rope at two angles to the vertical, $\phi$ and $\phi+d\phi$.
The displacement element is length $r.d\phi$. Note that it is at right angles to the rope.

Thank you for your reply @haruspex !

I guess it sort of makes sense to consider incremental changes in phi if we are trying prove the change in theta. I will try that!

Many thanks!

 

[member 731016]

Here are the new diagrams @haruspex !

I'm assuming the displacement vector is only at a right angle to the rope where it extends from (the red line in this case). I'm not sure if the displacement vector makes at right angle with the dark orange line (finial rope position)

Many thanks!

 

[jbriggs444]

I'm not sure if the displacement vector makes at right angle with the dark orange line (finial rope position)

$ds$ is (or behaves like) an infinitesimal. The incremental displacement is infinitesimally close to being at right angles to both the initial and final angles. Its angle differs from the perpendicular by only $d \phi$ at most.

But that is window dressing. Surely you are after the incremental work done. This should be the vector dot product of the force of gravity, $\vec{mg}$ and the incremental displacement, $\vec{ds}$.

 

[member 731016]

$ds$ is (or behaves like) an infinitesimal. The incremental displacement is infinitesimally close to being at right angles to both the initial and final angles. Its angle differs from the perpendicular by only $d \phi$ at most.

But that is window dressing. Surely you are after the incremental work done. This should be the vector dot product of the force of gravity, $\vec{mg}$ and the incremental displacement, $\vec{ds}$.

Thank you for your reply @jbriggs444 !

Oh ok that makes sense, now. I have added that too my new diagram (which is very not too scale):

Yes I think I am after the incremental work ($dW = \int_{\phi_1}^{\phi_2} Fr\cos\theta~d\phi$) in terms of phi which I will integrate from $\phi_1 = 0$ to $\phi_2 = 60$ (Where $\theta$ is the angle between the differential displacement and spider man's weight).

Would you please know how to get theta in terms of phi from the diagram? I think (by considering two cases from post #83) that $\theta = \phi + 90$

Many thanks!

 

[member 731016]

I think I may have found the answer!!!

First method:

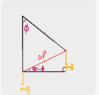
If we start with the big triangle,

Then,

$\phi + d\phi + 90 + \theta_2 = 180$
$\theta_2 = 90 - \phi - d\phi$

Now for the small triangle,

$90 + \theta_2 + \theta_1 = 180$
$\theta_1 = 90 - \theta_2$
$\theta_1 = 90 - (90 - \phi - d\phi)$
$\theta_1 = \phi + d\phi$

Therefore since $\theta = 90 + \theta_1$ (since $theta_1$ is vertically opposite)

Then $\theta = 90 + \phi + d\phi ≈ 90 + \phi$ since $d\phi$ is a differential

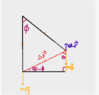
Second method:
I believe you could have also found $\theta_2$ from the medium size triangle,

Where in this case
$\theta_2 = 90 - \phi$
$\theta_1 = \phi + d\phi$
$\theta = 90 + \phi$ without having to make the approximation in the first method

Is my proof for $\theta = 90 + \phi$ geometrically correct?

Many thanks!

 

[jbriggs444]

Is my proof for θ=90+ϕ geometrically correct?

Yes. The concern with differentials is distracting and the drawings could be done more clearly -- in particular, labelling the angle you are calling $\theta$. But I agree with the conclusion.

It might make it easier to evaluate the resulting integral if you would write $\cos ( 90 + \phi )$ as $-\sin \phi$.

Personally, I would have looked at the formula for the projection of a vector normal to a [oriented] surface. That involves $\sin \theta$ where $\theta$ is the angle the vector makes with respect to the surface. In this case, the displacement vector makes an angle of $- \phi$ with respect to a horizontal surface. The projection thus involves $\sin -\phi = - \sin \phi$.

You can get the dot product of two vectors by taking the projection of one in the direction of the other and multiplying the magnitude of the one by the [signed] magnitude of the projection of the other.

Actually, I would have been sloppy with the sign convention, ignored the orientation of the surface, looked at $\sin \phi$ and then reasoned that the displacement and gravity are pointing generally away from each other and inverted the sign of the resulting path integral.

Actually, I would have recognized a conservative field, reasoned that all path integrals between a particular pair of endpoints across a conservative field will yield the same result and either picked a trivial path or computed the potential difference.

But we can definitely get to work evaluating the integral.

 

[member 731016]

Yes. The concern with differentials is distracting and the drawings could be done more clearly -- in particular, labelling the angle you are calling $\theta$. But I agree with the conclusion.

It might make it easier to evaluate the resulting integral if you would write $\cos ( 90 + \phi )$ as $-\sin \phi$.

Personally, I would have looked at the formula for the projection of a vector normal to a [oriented] surface. That involves $\sin \theta$ where $\theta$ is the angle the vector makes with respect to the surface. In this case, the displacement vector makes an angle of $- \phi$ with respect to a horizontal surface. The projection thus involves $\sin -\phi = - \sin \phi$.

You can get the dot product of two vectors by taking the projection of one in the direction of the other and multiplying the magnitude of the one by the [signed] magnitude of the projection of the other.

Actually, I would have been sloppy with the sign convention, ignored the orientation of the surface, looked at $\sin \phi$ and then reasoned that the displacement and gravity are pointing generally away from each other and inverted the sign of the resulting path integral.

Actually, I would have recognized a conservative field, reasoned that all path integrals between a particular pair of endpoints across a conservative field will yield the same result and either picked a trivial path or computed the potential difference.

But we can definitely get to work evaluating the integral.

Thank you so much for your reply @jbriggs444 !

Yeah true, there is a much easier method if I had recognized the conservative field! Sorry, what did you find distracting about my concern with differentials?

Was it the fact that first method I had to make an approximation and the second I did not (due to the choice of triangles)

I will post the integral

Many thanks!

 

[member 731016]

Here is the integration @jbriggs444 !

$W = -Fr\int_0^{60} \sin\phi d\phi$
$W = mgr\cos60= \frac {mgr}{2}$ which is correct!

Many thanks!

 

[jbriggs444]

Yeah true, there is a much easier method if I had recognized the conservative field! Sorry, what did you find distracting about my concern with differentials?

Well, a drawing of an isosceles triangle with two right angles is a bit distracting.

 

[member 731016]

Well, a drawing of an isosceles triangle with two right angles is a bit distracting.

Oh true! Thank for letting me know @jbriggs444 !