dla
- 27
- 0
Homework Statement
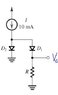
I am suppose to find an R value so that Vo=80mV given that both diodes are identical, conducting 10mA at 0.7 V and 100 mA at 0.8 V
Homework Equations
I = I_{s} e^{v/{V_{t}n}}
The Attempt at a Solution
I get that if the diodes are the same n, V_t and I_s are the same. So first I need to solve for n by using the equation and information above to create 2 equations assuming room temperature. Then I can make two equations from D1 and D2 and combine them to solve for V.
My main question is how did they know that Vo=V_2-V_1, voltage drop of diode 2 - voltage drop of diode 1. Why not the other way around? It might be simple but I am having a hard time seeing it any help will be much appreciated.
The circuit is attached. Thanks.