Five ropes in equilibrium supporting mass - calculate tension

[Adi1973]

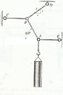
An object of mass 50 kg is supported at point A by five ropes as showin in the figure, and is in equilibrium. Determine the force in each rope.
Figure is attached.

Attempt at solution:

FBD is attached.

If the sides of the triangle formed by ROPE BD are in the relation of 5:3:4 respectively, the angle will be 53^o.

Gravitational force Fg = (50kg)(9.8m.s-2) South
= 490N South

The net horizontal and net vertical forces will equal zero as the system is not moving either right or left, or up or down (system is in equilibrium).

Therefore the sum of the horizontal forces pulling West will equal the sum of the horizontal forces pulling East:

FBC horizontal + FAB horizontal = FAE horizontal + FBD horizontal

The vertical force provided by the ropes will equal 490N North to balance the gravitational force exactly.

Therefore the sum of the vertical forces of the ropes will equal 490N:

FAB vertical + FBD vertical = 490N North

And that is as far as I got. Even colour coding the FBD diagram wouldn't help! Please could someone point me in the right direction. Something tells me that I have to put the vertical forces into some relation to one another to calculate how much each contribute to the 490N? Or not? Thank you for any help.

 

[Doc Al]

Do this: Draw a FBD for point A and see what you can deduce. Then do the same for point B.

 

[Adi1973]

Thanks Doc Al, so much appreciated. So, in essence, I treat it as two separate objects both in equilibrium in their own environments? Makes things simpler! I'm just not sure what the force is that is pulling point B - is it the gravitational force, or AB? I assumed gravitational force?

I attach my FBDs and here is my solution now (suspect there are still some things wrong though - looks a bit odd):

Point A:
F_{AB vertical} = 490N North (equilibrium, gravity)
F_{AB horizontal} = 1/2 (490) West (special right triangle 60^o-30^o-90^o)
= 245N West
sin60^o = 490N North / F_AB
Therefore F_AB = 566N 30^o North West
F_AE = - F_{AB horizontal} (equilibrium)
Therefore F_AE = 245N East

Point B:
F_{BD vertical} = 490N North (equilibrium, gravity)
tan53^o = 490N/F_{BD horizontal} (special right triangle 3-4-5)
Therefore F_{BD horizontal} = 369N North
sin53^o = 490N/F_BD
Therefore F_BD = 614N 37^o North East

F_BC = - F_{BD horizontal} (equilibrium)
Therefore F_BC = 369N West

 

[Doc Al]

So, in essence, I treat it as two separate objects both in equilibrium in their own environments? Makes things simpler!

Sure does.

I'm just not sure what the force is that is pulling point B - is it the gravitational force, or AB? I assumed gravitational force?

I don't understand this comment. The forces acting on point B are the tensions in the three ropes attached to point B.

I attach my FBDs and here is my solution now (suspect there are still some things wrong though - looks a bit odd):

Your FBD for point A looks good.

Regarding your FBD for point B:
- F_BC is correct
- F_BD is at the wrong angle
- Fg does not act on B! It's rope AB that attaches to B, so F_AB acts.
Redo that one.

Point A:
F_{AB vertical} = 490N North (equilibrium, gravity)
F_{AB horizontal} = 1/2 (490) West (special right triangle 60^o-30^o-90^o)
= 245N West
sin60^o = 490N North / F_AB
Therefore F_AB = 566N 30^o North West
F_AE = - F_{AB horizontal} (equilibrium)
Therefore F_AE = 245N East

This looks OK. A few comments:
They want the tensions in the ropes, which are just the magnitudes of the forces they exert. The directions, of course, are along the ropes. So, for example, let F_AB be the tension in rope AB. No need to specify direction when giving your answers.

I'd set it up like this, so that it's easy to see what you're doing:
ΣFx = 0
F_AE - F_AB cos(60) = 0
F_AB cos(60) = F_AE

ΣFy = 0
F_AB sin(60) - Fg = 0
F_AB sin(60) = Fg

Careful about rounding off your calculations. I'd only round off at the last step.

 

[Adi1973]

Thank you very much for the help! I can finish it now myself. I really appreciate the amazing responses, it has really cleared things up quickly.