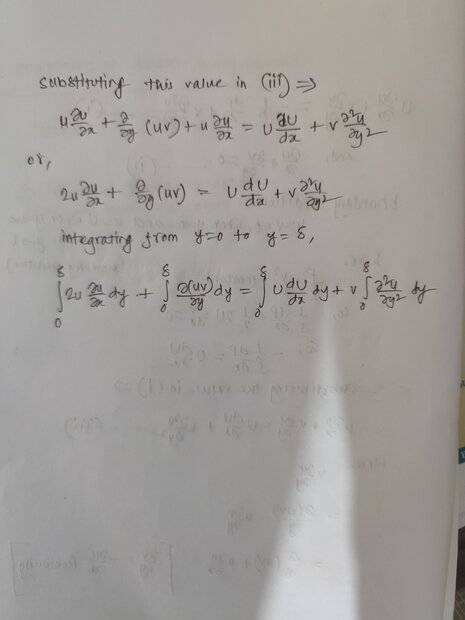SUMMARY
The discussion focuses on the Prandtl Boundary Layer Equation in the context of steady laminar flow. It emphasizes that the Bernoulli equation is applicable only in inviscid flow conditions, where boundary layers do not exist. The key takeaway is that while Bernoulli's principle can be used in the free stream away from the boundary, it cannot be applied within the boundary layer itself. Understanding this distinction is crucial for correctly analyzing fluid flow in boundary layer theory.
PREREQUISITES
- Understanding of the Prandtl Boundary Layer Equation
- Familiarity with steady laminar flow concepts
- Knowledge of Bernoulli's equation and its limitations
- Basic principles of fluid dynamics
NEXT STEPS
- Study the derivation and applications of the Prandtl Boundary Layer Equation
- Learn about the characteristics of steady laminar flow in fluid dynamics
- Explore the limitations and proper applications of Bernoulli's equation
- Investigate boundary layer theory and its implications in engineering
USEFUL FOR
Students and professionals in fluid dynamics, mechanical engineers, and anyone involved in analyzing laminar flow and boundary layer phenomena.