Flux due to infinite long wires

[Saitama]

Homework Statement

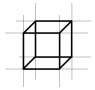
Twelve infinite long wires of uniform linear charge density (λ) are passing along the twelve edges of a cube. Find electric flux through any face of cube. (see attachment)

Homework Equations

The Attempt at a Solution

I have actually solved the problem but I think there's a more simpler way.

Okay, I figured out that electric field due only four out of twelve wires will contribute to the electric flux through any face. Let's consider the bottom face. The flux passing through this face is due to only four wires of the top face.

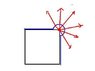
Calculating flux due to a single wire. (see attachment 2)
In the figure $x=l \tan \theta$. Or, $dx=l \sec^2 \theta d\theta$.
Electric field due to this wire, \vec{E}=\frac{\lambda \cos \theta}{2 \pi \epsilon_o l}
Value of the differential area is
\vec{dA}=(l)(dx)=l^2 \sec^2 \theta d\theta
Flux is the dot product of the electric field vector and area vector.
d\phi=\vec{E} \cdot \vec{dA}
d\phi=\frac{\lambda \cos \theta}{2 \pi \epsilon_o l} \cdot l^2 \sec^2 \theta d\theta \cdot \cos (180-\theta)
\phi=\int_{0}^{\pi/4} \frac{\lambda l}{2 \pi \epsilon_o} d\theta
Solving this, the flux due to a single wire is
\phi=\frac{\lambda l}{8 \epsilon_o}
Last step is to multiply it by 4.

I think that there is a much easier way instead of doing the math. Most of the questions I have done based on finding flux through cube or its faces have some kind of symmetry and I guess that this question too involves some trick which I can't figure out.

Any help is appreciated. Thanks!

 

[ehild]

What abou Gauss' Law?

ehild

 

[Saitama]

What abou Gauss' Law?

ehild

How?

What should be the gaussian surface?

 

[BruceW]

I can think of one way. Think of the most obvious Gaussian surface. I get a different answer to your calculation. I don't know why you have assumed that only electric field due to the wires on the opposite face contributes..

Edit: a hint: don't be surprised if the answer depends on the limit in which you take the Gaussian surface.

 

[Saitama]

I don't know why you have assumed that only electric field due to the wires on the opposite face contributes..

I sketched the field lines due to each wire and found that only four wires contribute to electric flux through any face.

 

[BruceW]

hmmm... what about the four wires which extend perpendicular to the face?

Also, the symmetry argument I am thinking of only works for the flux through the face which is defined either just inside or just outside the cube... I now realize that you are trying to find the flux through an area which is exactly on the plane of one of the faces, and contained within the boundary of the wire. So the symmetry argument I was thinking of doesn't work in that case.

 

[ehild]

How?

What should be the gaussian surface?

The surface of the cube?

ehild

 

[BruceW]

I think the problem is that if it is exactly the surface of the cube, then what is the enclosed charge? There is no problem if we are talking about flux just inside or outside the cube, but flux at exactly the cube faces is more difficult.

edit: for sure, the electric field is not continuous at the face of the actual cube. (unless we make the wires have finite width, but since we are not told this, I think he is meant to assume the wires are effectively dirac-delta 'functions').

 

[Saitama]

hmmm... what about the four wires which extend perpendicular to the face?

Draw the field lines due to one of those wires. The field lines are always normal to the direction of area vector.

The surface of the cube?

ehild

I am still at loss. We have got a line charge here. If it was a point charge, it would have been easy to calculate the flux (given that it is at one of points where flux can be calculated using symmetry) but I don't get how we can calculate flux of a line charge using symmetry arguments.

 

[BruceW]

Draw the field lines due to one of those wires. The field lines are always normal to the direction of area vector.

No. It would be, if the wire was infinitely long, but these wires are not infinitely long.

I am still at loss. We have got a line charge here. If it was a point charge, it would have been easy to calculate the flux (given that it is at one of points where flux can be calculated using symmetry) but I don't get how we can calculate flux of a line charge using symmetry arguments.

The idea is that you can calculate the flux through the face due to all the wires. (but we can only do this for the face just inside and just outside the cube). Use a Gaussian cube just inside the actual cube. What is the charge enclosed? And by symmetry, what does this tell you about the flux through each face? And also, do this for a Gaussian cube just outside the actual cube.

Edit: darnit. I'm so sorry, I thought the wires were supposed to be not infinitely long. Sorry about that. I should have read your post more carefully.

 

[BruceW]

I'm pretty sure the symmetry argument will still work even though the wires are infinitely long, because there is still a symmetry in the system. But as I said, this only works for the flux just inside the actual cube or just outside the actual cube. And then your method gives the flux which is exactly on the face of the actual cube. I can't think of any way to get the answer for exactly on the face of the cube, using symmetry..

 

[ehild]

You do not need to calculate the electric field. But you can use symmetry. Is the flux different at the different faces of the cube?

ehild

 

[Saitama]

You do not need to calculate the electric field. But you can use symmetry. Is the flux different at the different faces of the cube?

ehild

Due to a single wire, the flux is zero through four faces and equal for the other two faces.

 

[ehild]

I mean due to all wires. ehild

 

[Saitama]

I mean due to all wires.


ehild

Then its same for all the faces.

 

[BruceW]

yep :)

 

[ehild]

And what is the whole flux for a surface just enclosing the cube?

 

[Saitama]

And what is the whole flux for a surface just enclosing the cube?

It would be 6 times the flux through each face but for that I will have to find the flux through each face.

 

[BruceW]

yes, it is 6 times the flux through each face. And the key is to use Gauss' law now. I'm still stressing that this is for flux just outside the face.

Edit: I'm sure it will seem obvious, once you realize it.

 

[ehild]

It would be 6 times the flux through each face but for that I will have to find the flux through each face.

What does Gauss' Law state?

ehild

 

[Saitama]

What does Gauss' Law state?

ehild

\int \vec{E} \cdot \vec{dA}=\frac{q_{enclosed}}{\epsilon_o}

 

[ehild]

What is the enclosed charge if you cover the cube with a closed cubical surface just outside the faces?

ehild

 

[Saitama]

What is the enclosed charge if you cover the cube with a closed cubical surface just outside the faces?

ehild

$12λl$?

 

[ehild]

yes.

 

[Saitama]

yes.

The flux through the whole cube is $12\lambda l/ \epsilon_o$. Then flux through a single face is $\frac{2\lambda l}{\epsilon_o}$ but this is not the right answer.

 

[ehild]

Looks, one solution is wrong. Did you use the correct expression of the electric field due to a single wire?

ehild

 

[Saitama]

Looks, one solution is wrong. Did you use the correct expression of the electric field due to a single wire?

Yes, I am sure that I have used the correct expression for the electric field.

 

[ehild]

What you wrote as E it was the normal component of the electric field, and you used it correctly. So I do not know what is wrong. Perhaps the Gaussian surface at the edges. The wires had to be wrapped by the surface, and these cylindrical surfaces add contribution to the flux.

ehild

 

[BruceW]

you have the correct answer for the flux just outside the face. To summarise:
flux just outside = 2 \lambda l / \epsilon_0
flux just inside = zero
flux exactly on the face = \lambda l /2 \epsilon_0
the electric field (and flux) is not continuous, as I said. Which is why there is the discontinuous 'jumps' between these three answers. And I don't think it is easy to get the answer for flux exactly on the face, by using symmetry. But you have calculated it by using the method of adding electric field contributions from each wire. So all is good.

Edit: to make this clear, all three answers are correct. It just depends on whether you want to talk about the flux just inside, just outside, and exactly on the face.

 

[ehild]

The Gaussian surface has to wrap up the whole cube, including the edges. The flux across the cylindrical surfaces add to the flux of the faces. If the radius of the wrapping cylinders is δ the flux of a single wire across its own 3/4 cylindrical wrapping surface is

ψ=λ/(2πε₀ δ) L 3/4 (2πδ)= 3/4 λL/ε₀.
As δ tends to zero, the flux of the other edges through the cylindrical surfaces tend to zero.

The flux across a single face is Φ. So the total flux is 12λL=6Φ+12[3/4 λL/ε₀---> Φ=λL/(2ε₀)

ehild