ehild said:
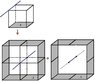
The Gaussian surface has to wrap up the whole cube, including the edges. The flux across the cylindrical surfaces add to the flux of the faces. If the radius of the wrapping cylinders is δ the flux of a single wire across its own 3/4 cylindrical wrapping surface is
ψ=λ/(2πε0 δ) L 3/4 (2πδ)= 3/4 λL/ε0.
As δ tends to zero, the flux of the other edges through the cylindrical surfaces tend to zero.
The flux across a single face is Φ. So the total flux is 12λL=6Φ+12[3/4 λL/ε0---> Φ=λL/(2ε0)
ehild
Yes! very nice. Maths is a creative subject :) It takes imagination for problems like this. There is also the issue of how the cylinders join up at the vertices of the cube, but when we take the limit of very small cylinders, the length of cylinder which is effected by the edge effect tends to zero, so there is not a problem.
Also, I am glad to see that this way of doing the problem gives the same answer as Pranav's original post. It is always nice in physics when two different methods agree. Yeah, so this method gives the 'flux exactly on the face' answer.
I'll see if I can explain it. The Gaussian surface is almost a cube, where the faces coincide with the faces of the actual cube, except near the edges, where the Gaussian surface is 3/4 of a cylinder going around the wire. We know the total flux, because we know enclosed charge. Some of the flux will go out of the faces, and some of the flux will go out of the little cylinders at the edges. Now we take the limit that the little cylinders get very little. (i.e. the distance from the cylinder to the wire tends to zero). You might think that the flux through them will tend to zero because they are very little. But this does not happen because as the cylinder gets smaller, it gets closer to the wire, so the electric field tends to infinity. So in the limit of very small cylinders, we get a finite answer for the flux coming out of them.
As ehild said, as we make the cylinders very small, the flux through each cylinder is due to only the electric field coming from the wire it is very close to. This is because the electric field from the other wires is finite, and the area of the cylinder tends to zero, so the flux due to the other wires tends to zero. This makes it fairly easy to calculate the flux through each wire.
So now you have the total flux and the flux through each wire, so you can calculate how much flux goes through the faces. (It is just what is left over). Also, as the cylinders get very small, the area of the face tends to the area of the face of the actual cube. so what we have really done is an improper integral.
Hope that explanation helped. I think the more times you practice electrostatics problems, using Gaussian surfaces, the better you get at 'guessing' what kind of Gaussian surface would be most useful. The book 'Introduction to electrodynamics' by Griffiths might be useful. I don't know if there are practice questions in the book though.
One last thing: you could use a slightly different Gaussian surface which uses 1/4 cylinders, which are inside the wires. In this case, the enclosed charge is zero, so the total flux is zero. And so the flux through the cylinders is equal and opposite to the flux through the faces, so you can also work out the answer this way, which gives the same answer.
Edit: also, I have attached a picture of ehild's method. The picture is a slice through the cube. i.e. the wires are coming out of the page, and are enclosed by the cylinders.

 .
.