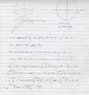- #1
schmiggy
- 38
- 0
Homework Statement
I've attached an image with the entire question.
Homework Equations
Attached an image with relevant equations. Can't use Gauss' Divergence
The Attempt at a Solution
In the attached image I've also included the start of my calculations, I just need to see if my double integral is correct.. if it is I can easily compute it, and have done so.. however the answer I got made me doubt my working.
Naturally I would replace the x and y with rcos(theta) and rsin(theta) respectively which would become 2r^2, as cos^2(theta) + sin^2(theta) = 1.
Anyway, the answer I got using the double integral in the attached image was 384pi and can't help but feel like I'm way off. Any guidance would be greatly appreciated, thanks!