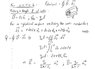Flux out of a Cylindrical Cable

[jegues]

Homework Statement

A coaxial transmission line has an inner conducting cylinder of radius a and an outer conducting cylinder of radius c. Charge ql per unit length is uniformly distributed over the inner conductor and -ql over the outer. If dielectric $\epsilon_{1}$ extends from r=a to r=b and dielectric $\epsilon_{2}$ from r=b r=c, find the electric field for r<a, for a<r<b, for b<r<c and for r>c. Take the conducting cylinders as infinitesimally thin.

Homework Equations

The Attempt at a Solution

For r<a there is no charge enclosed thus the flux is 0 so E is also 0

Here is the solution they give for a<r<b. (see figure attached)

I am confused as to how he determines the components of the vector $d\vec{S}$. Is there a picture that will explain this?

Thanks again!

 

[quietrain]

http://hyperphysics.phy-astr.gsu.edu/hbase/sphc.html
scroll down to cylindrical polar coordinates

http://en.wikipedia.org/wiki/Cylindrical_coordinate_system#Line and volume elements
scroll down to line and volume elements section, of surface element

that is how he got the ds which is the surface element of cylinder in cylindrical coordinates.

i can't help you on the rest, because i forgot my electromag already ::(

 

[jegues]

http://hyperphysics.phy-astr.gsu.edu/hbase/sphc.html
scroll down to cylindrical polar coordinates

http://en.wikipedia.org/wiki/Cylindrical_coordinate_system#Line and volume elements
scroll down to line and volume elements section, of surface element

that is how he got the ds which is the surface element of cylinder in cylindrical coordinates.

i can't help you on the rest, because i forgot my electromag already ::(

The wiki gives me the line, surface and volume elements but I don't want to have to memorize them.

Isn't there a more intuitive way of understanding this as opposed to memorizing it?

 

[quietrain]

you are not suppose to memorize them, they should be given in the exams.

you are suppose to understand how to get them

take a look at these for more info

http://www.math.ubc.ca/~feldman/m227/coordsys.pdf

http://www.math.montana.edu/frankw/ccp/multiworld/multipleIVP/cylindrical/learn.htm