Amith2006
- 416
- 2
# Diameter of a Plano-convex lens is 6 cm and the thickness at the center is 3 mm. If the speed of light in the material of the lens is 2 x 10^8 m/sec, what is the focal length of the lens?
I solved it in the following way:
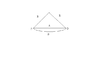
Let R be the radius of curvature of the convex surface.
Given that AB = 3 mm = 0.3 cm, AD = CD/2 = 3 cm, refractive index(n) = 1.5
By the property of circles,
AB = (AD^2)/(2R)
Therefore, R = (AD^2)/(2AB)
= 9/(2 x 0.3)
= 15 cm
According to thin lens formula,
1/f = (n – 1)/R
Solving I get,
f = 30 cm
Is it right?
I solved it in the following way:
Let R be the radius of curvature of the convex surface.
Given that AB = 3 mm = 0.3 cm, AD = CD/2 = 3 cm, refractive index(n) = 1.5
By the property of circles,
AB = (AD^2)/(2R)
Therefore, R = (AD^2)/(2AB)
= 9/(2 x 0.3)
= 15 cm
According to thin lens formula,
1/f = (n – 1)/R
Solving I get,
f = 30 cm
Is it right?