Following Schwartz's argument re: measuring (g-2)

[GreenPenInc]

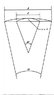
I've been reading Melvin Schwartz's mostly excellent book, Principles of Electrodynamics. He has a section on measuring (g-2) for the muon, and I'm trying to follow the argument. I've attached the figure for reference.

He takes the approach of considering an instantaneously comoving frame of reference (this is all within the context of special relativity) and measuring the various effects. Basically, for illustration sake, the problem we're considering is that of a particle in a uniform magnetic field $B$, moving at right angles to the magnetic field, so in the lab frame it should be in uniform circular motion. In the boosted frame, there is an electric field $\bar{E} = \gamma \beta B$, and the magnetic field there is $\bar{B} = \gamma B$ , and if we stayed in this frame (instead of moving to the next instantaneously comoving frame) the motion would be a cycloid.

Schwartz analyzes an infinitesimal portion of the orbit in each case, as follows. He says that in each frame, the path would appear to be a segment of arc, but in the comoving frame that segment is 'foreshortened'. In the attached figure, he's drawn both arc segments on top of each other.

Here's my problem: it seems to me that in the instantaneously comoving frame, at the instant when t=0, the particle has zero velocity. (We're measuring the velocity in a frame which has the same velocity as the particle, ergo it starts from rest in the primed frame.) Now the electric field is at right angles to the boost direction, so the initial motion should all be perpendicular to the boost. But in the lab frame, that infinitesimal portion of the arc should be along the boost direction, right? So it seems like the arc in one frame is perpendicular to the arc segment in the other frame, and so I don't understand why he draws them on top of each other.

It's not just a small point, either. Based on this diagram, he equates $s =s^\prime$, since dimensions perpendicular to the boost don't contract. Since $d = \gamma d^\prime$, he can relate $d\theta$ to $d\theta^\prime$, and thereby relate the (instantaneous) angular velocity in the primed frame, to the cyclotron frequency in the lab frame. It seems pretty central to his argument.

Can anyone help me out here? i.e. is my basic analysis -- that the arc segments are perpendicular, and that this invalidates his argument about $s=s^\prime$ -- essentially correct?

Best of all would be if someone who has access to the book (it's Dover and highly rated, so probably several people here have it) can explain to me what the heck he's talking about in section 4-11. It seems like really interesting physics and I'd love to learn it. :)

Thanks!
Chip

 

[GreenPenInc]

No replies? In retrospect I can understand that -- I made it hard for people without the book to follow the argument. Let me now reproduce it here; hopefully, along with the attached figure, that should grant everything you need to help me out.

To follow what is going on, it would be most convenient to move along with a coordinate system attached to the muon. Inasmuch as the muon's own coordinate system is not an inertial system, we might imagine ourselves within a bit of difficulty here, but we can get out of it by a very simple ruse. We will follow the muon's progress with a succession of inertial systems, each moving with the muon's speed, and tangential to its orbit at some point. We will then relate the observations within one coordinate system to those within the next system down the line ntil the particle finally leaves the field altogether.

We will make the simplifying assumption that the charged particle is moving with speed $v$ at right angles to the field and that the motion all takes place within one plane. (Needless to say, this assumption is not precisely true in reality and a careful analysis of the orbits is necessary.) Subject to this assumption, an observer in each of our moving coordinate systems sees a magnetic field equal to $\gamma \vec{B}$ where $\vec{B}$ is the laboratory field at that point and $\gamma = 1/\sqrt{1-v^2/c^2}$.

We begin by examining an infinitesimal portion of the particle's orbit as seen from both the laboratory system $\Sigma$ and from the moving system $\Sigma^\prime$ which is tangential to the particle's orbit at this point (see Fig. 4-12). In either case the orbit appears to be a segment of arc, but within $\Sigma ^\prime$ it appears much foreshortened and hence of smaller radius than in $\Sigma$ . The sagitta of the arc is $s$ as seen in $\Sigma$ and $s ^\prime$ as seen in $\Sigma ^\prime$ . The chord of the arc is $d$ as seen in $\Sigma$ and $d ^\prime$ as seen in $\Sigma ^\prime$ . Obviously $s ^\prime = s$ and $d ^\prime = d / \gamma$ . If $d\theta$ is the angle of arc as seen by $\Sigma$ and $d\theta ^\prime$ is the angle of arc as seen by $\Sigma ^\prime$ , then

$\frac{d\theta ^\prime }{d\theta } = \frac{s ^\prime d}{s d ^\prime } = \gamma$

Now what about the time to go from one end of the segment to the other? Since $\Sigma ^\prime$ is the particle's rest frame at the moment, we can write

$dt = \gamma dt ^\prime$

Hence the rate of change of direction as seen by $\Sigma ^\prime$ can be related to the rate of change of direction as seen by $\Sigma$ .

$\frac{d\theta ^\prime}{dt ^\prime} = \frac{\gamma ^2 d\theta }{dt}$

But $d\theta / dt$ is just the cyclotron frequency of the particle, $eB/mc$, where $B$ and $m$ are as measured in the laboratory. This leads to

$\frac{d\theta ^\prime }{dt ^\prime } = \frac{ \gamma ^2 e B}{\gamma m_0 c} = \frac{\gamma e B}{m_0 c}$

Next we must find through what angle $d\varphi ^\prime$ the spin has precessed during the same time interval $dt ^\prime$ . The magnetic field as seen by $\Sigma ^\prime$ is $\gamma B$ , and hence the Larmor frequency is

$\frac{d\varphi ^\prime }{dt ^\prime } = g \frac{e \gamma B}{2 m_0 c}$

Thus the angle between spin and orbit direction, as seen by $\Sigma ^\prime$ , has changed from one end of the arc to the other by an amount

$d(\varphi ^\prime - \theta ^\prime ) &=& (g-2)\frac{e \gamma B}{2 m_0 c}dt ^\prime =(g-2)\frac{eB\,dt}{2m_0c}$

We now transform to the moving system which is tangential to the next segment of arc ($\Sigma ^{\prime \prime }$ ). Since the relative velocity of $\Sigma ^{\prime\prime}$ and $\Sigma ^\prime$ is infinitesimal, the angle between spin and orbit at any given point on the orbit does not change with this transformation. Thus we have

$(\varphi ^\prime - \theta ^\prime )_{end of first segment} = (\varphi ^{\prime\prime} - \theta ^{\prime\prime} )_{beginning of second segment}$

Following the particle over the second arc, as seen from $\Sigma ^{\prime\prime}$ , we come up with the same equation for the change in angle between orbit and spin direction. We continue this procedure until we leave the magnet. Adding together all the changes in angle between spin and direction of motion, we conclude that
$\Psi ^\prime = (g-2) \frac{e\bar{B}}{2m_0c}t$
where $\Psi^\prime$ is the angle between the direction of muon spin and direction of motion upon leaving the magnet, as seen by an observer moving with the muon, $\bar{B}$ is the average field experienced by the muon and $t$ is the time spent in the magnet.

Now that it's placed in a bit of context, does that make it any easier for people to help me evaluate the argument? Again: I don't get how he can draw the arc segments to be parallel at their centres, when in an instantaneously comoving frame, the force at that instant should be perpendicular to the boost direction. (And obviously, the boost direction is the direction of motion in the lab frame.)

His argument for the length of the arc being contracted seems to be based on length contraction along the direction of the boost, where the perpendicular dimensions (here, $s = s ^\prime$ ) don't contract. Can anyone help me understand what he's trying to say?

Thanks in advance!

 

[pervect]

It sounds like Schwarz is trying to explain Thomas precession.

I'm not sure I particularly care for or follow his explanation. Online, you might try http://bohr.physics.berkeley.edu/classes/221/0708/notes/thomprec.pdf for an alternate explanation. Jackson also has a section about Thomas Precession in "Classical Electrodynamics", and many GR books will disuss it (for example, MTW's "Gravitation").

A very simple overview would be this. A particle held in a circular orbit can be modeled as being subjected to a large number of Lorentz boosts. The effect of multiple Loretnz boosts can be described as taking a matrix product of the Lorentz transformation matrices (or the equivalent in tensor notation). The matrix product of the infinite number of Loretnz boosts of an object accelerated around in a circle is, however, not the identity matrix, but a rotation. This is easy to say, but it gets a bit more involved to prove.

 

[GreenPenInc]

I think I've come to understand this problem to my satisfaction now.

If we stayed in one instantaneously comoving frame (instead of always jumping to the next frame, etc.) we would see the path of the particle as following an ellipse, which itself is moving at a constant velocity. If we 'correct' for that motion (in the Galilean sense), we do indeed see that the length of the arc, at the point where this frame is the comoving one, is 'foreshortened' by the Lorentz contraction, just as Schwartz says. Then we can follow his whole argument.

Basically, the problem is that he doesn't mention that the contracted path which the particle follows is itself moving, and this led to all my difficulties in understanding. Without taking that into account, the particle indeed stays still to first order in time, but that's not what's relevant.

Thanks for the great reference. I skimmed it, and I'll probably check it out in greater detail when I have some time.